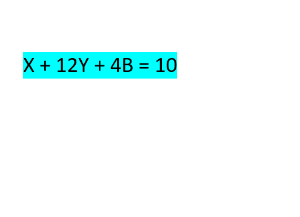Starting with system of equations:
x+2y+10a+0b = 30
2x+4y+6a+0b = 20
2x+8y+0a+6b=40
We need to find the values for a and b. Problem is we have three equations and four unknowns.
Write an augmented matrix using the above equations.
\left|\begin{array}{cccc | c} 1 & 2 & 10 & 0 & 30 // 2 & 4 & 6 & 0 & 20 // 2 & 8 & 0 & 6 & 40 \end{array}\right|
Begin row-reduction techniques.
\left|\begin{array}{cccc | c} 0 & 0 & 7 & 0 & 20 // 1 & 2 & 3 & 0 & 10 // 2 & 8 & 0 & 6 & 40 \end{array}\right|
9 Comments
Unknown User (annesch)
What is the task exactly?
Unknown User (brsmithe)
I think I'll just plug the augmented matrix into Wolfram
Unknown User (brsmithe)
Simplifies to
{{1,0,0,-3,-120/7}, {0,1,0,3/2,65/7},{0,0,1,0,20/7}}
Unknown User (brsmithe)
So a = 20/7
Unknown User (brsmithe)
x-3b = -120/7
2y+3b = 120/7
so
x+2y=10/7
x+y-1.5b=-55/7
then
10/7 + y - 1.5b +-55/7
y-(3/2)b=-65/7
FINALLY
b=(130/21)-(2/3)y
Unknown User (brsmithe)
Wait! Using the solution for A, rewrite the equations by moving A to the side of constants. I get
x+2y+0b = (30-10a)
2x+4y+0b = (20-6a)
2x+8y+6b = 40
Wait, never mind. the first two equations are linearly dependent on each other
Unknown User (annesch)
Here is my solution page:
A-Team, solution method 2
Unknown User (brsmithe)
With the new blue equations, I solved for the b variable! Using wolframalpha row reduction
B=130
A still equals 20/7
New equations:
10x+6y+2a=10
x+12y+4b=10
4x+4y+10b=30
Unknown User (brsmithe)
Here are the other images!