Introduction
Cornell SLAC Pixel Array Detector (CSPAD) is an imaging X-ray detector made of silicon sensors (2x1) covering about 20x20cm² surface, as shown in the plot:
Pixel coordinates in 2x1 sensor chip are known with sub-micrometer precision. Construction of the detector allows significant freedom in relative positions of 2x1 sensors. To get precise pixel positions in the detector the 2x1 sensor coordinates needs to be calibrated. In this note we describe geometry of the CSPAD detector, optical and quad alignment procedure, parameters, and software providing access to precise geometry information.
2x1 Sensor Geometry
The 2x1 sensor geometry was tested with microscopic measurement. Two slides from Chris Kenney's presentation shows the pixel sizes:
The same slides in PDF format.
Important 2x1 features:
- Number of rows x columns = 185 x 388. (In DAQ notation of rows and columns is interchanged...)
- Most of pixels have size 109.92 x 109.92 um².
- Gap between two ASICS is covered by the two rows of elongated pixels with size 109.92 x 274.8 um².
- Two versions of sensors have different dimensions between corners, so it is reasonable to define pixel coordinates w.r.t. the sensor center.
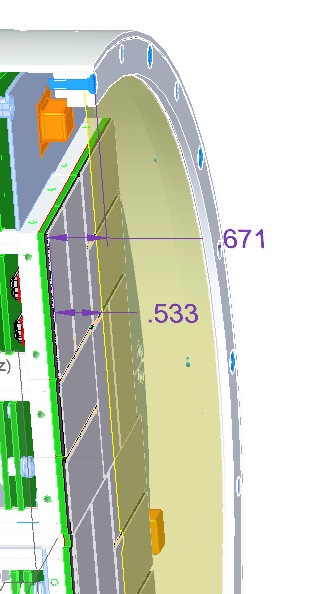
Shield to sensor distance
Chart of CXI Camera1 provided by Serge Guillet on 2017-06-12.
Optical measurement
Optical measurement is conducted by Gabriel Blaj. Detector or its quad is installed on microscope table and 3-d coordinates of all 2x1 sensor corners are measured with precision about 8um (RMS) in x-y plane. All corners in the measurement are numerated in arbitrary order. It is expected that numeration order should be the same for different measurements. This procedure depends on CSPAD construction;
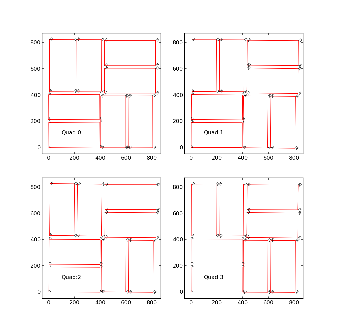
- For CSPAD with movable quads (i.e. for CXI) optical measurement is done separately for each quad. The numeration of corners is shown in the plot:
The same plots in PDF format: CSPAD quad metrology and CSPAD pixel layout in quads.
For each quad measurement is started from the point #1 which in assembled detector is closest to the beam. The 1-st point (x,y,z) coordinates are re-set to (0,0,0) in the beginning of measurements. At the end, it is checked that the 1-st point coordinates are reproduced within precision of measurement.
The order of points in optical measurement does not coincide with numeration of 2x1 in DAQ, as shown in the plot (and in PDF file):
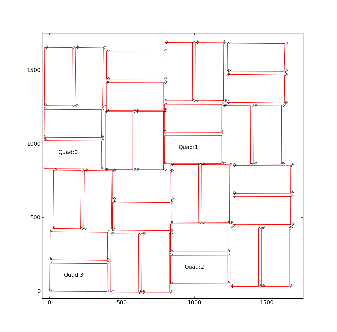
- For CSPAD with fixed quad geometry (i.e. for XPP) optical measurement is done for entire detector. The numeration of corners in this case is shown in the file XPPMetrologyAnnotated.pdf and in the plot:
The 1-st corner of the 3-rd quad (x,y,z) coordinates are re-set to (0,0,0) in the beginning of measurements. At the end, it is checked that the 1-st point coordinates are reproduced within precision of measurement.
Corner coordinates are measured in micrometers (um) and are saved in the xlsx format table, also containing numeration of quads and points. Then, xlsx format table is converted to the text file format in order to use it in python script.
Example of tables for CXI:
Example of tables for XPP:
- Metrology in XLSX
- Metrology in TXT Python script converts this table to the table with standard numeration of points in quads:
- Metrology in standard TXT
Then, text table with "standard" numeration of points in quads is feed to the python script which provides quality check of optical measurement and evaluates the alignment parameters for quads. In the beginning, this script changes the numeration of points adopted in optical measurement to numeration of 2x1 used in DAQ. Further, all calibration parameters are associated with numeration of 2x1 sensors and quads in DAQ.
Quality Check Procedure
For quality check of optical measurement we calculate
S1 - 1st short side length of 2x1
S2 - 2nd short side length of 2x1
L1 - 1st long side length of 2x1
L2 - 2nd long side length of 2x1
D1 - 1st diagonal of 2x1 between corners 1 and 3
D2 - 2nd diagonal of 2x1 between corners 2 and 4
dS and dL are the deviations of the 1st and 2nd corner along the short and long sides, respectively. The sign of all dS are chosen in order to provide correct sign for the tilt angle (the same direction for all 2x1 sensors).
<dS/L> - the tilt angle of 2x1 averaged over two sides in radians.
angle(deg) - the same angle in degrees.
dD = D1 - D2
d(dS) = dS1 - dS2
d(dL) = dL1 - dL2
dz3(um) - signed distance from 2x1 sensor plane and corner 3, where the 2x1 sensor plane contains the corner points p1, p2, and p4. This plane is defined by the vectors v21=p2-p1, v41=p4-p1, and their orthogonal vector
vort = [v21 x v41].
Scalar product with normalization defines the distance from point 3 to the 2x1 plane containing 3 other points:
dz3 = (v31 * vort) / |vort|.
Quality check parameters expected for perfect geometry:
S1=S2, L1=L2 - the 2x1 sides should have equal length and width,
D1=D2 - the 2x1 diagonals should be equal,
dS1 = dS2 ? (388/185)*dL1 = (388/185)*dL2 - tilt angle should provide consistent deviation for all corners,
dD=0, d(dS)=0, and d(dL)=0 - within precision of measurement.
dz3(um) = 0
Everything, excluding <dS/L> and angle(deg), are in micrometers.
Example of the table with quality check results:
pair: S1 S2 dS1 dS2 L1 L2 dL1 dL2 <dS/L> angle(deg) D1 D2 dD d(dS) d(dL) dz3(um) Quad 0 pair: 0 20891 20913 200 222 43539 43541 -102 -100 0.00485 0.27766 48298 48297 1 -22 -2 2.981 pair: 1 20910 20894 293 277 43540 43535 -127 -132 0.00655 0.37506 48302 48289 13 16 5 -23.986 pair: 2 20890 20906 99 83 43536 43536 42 42 0.00209 0.11976 48290 48293 -3 16 0 -3.034 pair: 3 20897 20895 131 133 43545 43543 65 63 0.00303 0.17369 48299 48297 2 -2 2 6.003 pair: 4 20911 20896 -30 -45 43549 43547 17 15 -0.00086 -0.04934 48303 48306 -3 15 2 -5.994 pair: 5 20901 20898 10 7 43540 43544 -8 -4 0.00020 0.01119 48296 48299 -3 3 -4 9.993 pair: 6 20904 20903 104 105 43536 43540 55 59 0.00240 0.13752 48302 48290 12 -1 -4 52.002 pair: 7 20901 20901 -7 -7 43545 43543 -3 -5 -0.00016 -0.00921 48299 48301 -2 0 2 14.001 Quad 1 pair: 0 20913 20914 -343 -342 43540 43550 165 175 -0.00787 -0.45066 48313 48303 10 -1 -10 -24.002 pair: 1 20898 20901 -145 -142 43548 43551 62 65 -0.00330 -0.18880 48300 48309 -9 -3 -3 -23.005 pair: 2 20895 20903 -151 -159 43535 43532 -74 -77 -0.00356 -0.20400 48289 48291 -2 8 3 -17.995 pair: 3 20872 20909 -235 -272 43341 43354 -37 -24 -0.00585 -0.33507 48201 48036 165 37 -13 -13.010 pair: 4 20940 20904 -455 -491 43527 43554 214 241 -0.01086 -0.62242 48309 48309 0 36 -27 1.101 pair: 5 20910 20903 -302 -309 43546 43546 145 145 -0.00702 -0.40196 48304 48307 -3 7 0 6.016 pair: 6 20901 20919 -421 -439 43529 43539 -213 -203 -0.00988 -0.56593 48296 48298 -2 18 -10 -8.026 pair: 7 20907 20907 -452 -452 43548 43539 -201 -210 -0.01038 -0.59475 48315 48294 21 0 9 -8.982 Quad 2 pair: 0 20914 20914 -25 -25 43536 43540 10 14 -0.00057 -0.03290 48300 48300 0 0 -4 -11.013 pair: 1 20901 20897 7 3 43546 43536 -1 -11 0.00011 0.00658 48293 48300 -7 4 10 4.036 pair: 2 20899 20903 -256 -260 43533 43539 -127 -121 -0.00593 -0.33954 48293 48294 -1 4 -6 -1.023 pair: 3 20912 20904 -210 -202 43540 43547 -106 -99 -0.00473 -0.27106 48300 48306 -6 -8 -7 24.004 pair: 4 20910 20903 -543 -550 43535 43536 261 262 -0.01255 -0.71923 48298 48299 -1 7 -1 0.004 pair: 5 20904 20905 -241 -240 43538 43544 111 117 -0.00552 -0.31647 48298 48301 -3 -1 -6 -6.024 pair: 6 20903 20902 21 22 43539 43543 8 12 0.00049 0.02829 48298 48298 0 -1 -4 8.999 pair: 7 20902 20903 82 81 43546 43547 35 36 0.00187 0.10723 48300 48306 -6 1 -1 9.995 Quad 3 pair: 0 20902 20898 -82 -86 43536 43543 30 37 -0.00193 -0.11054 48289 48302 -13 4 -7 1.994 pair: 1 20900 20904 79 83 43548 43541 -35 -42 0.00186 0.10658 48301 48301 0 -4 7 -17.993 pair: 2 20912 20894 181 199 43536 43535 97 96 0.00436 0.25005 48298 48289 9 -18 1 10.011 pair: 3 20912 20905 119 126 43539 43538 57 56 0.00281 0.16121 48296 48301 -5 -7 1 -16.000 pair: 4 20894 20912 -454 -436 43534 43545 212 223 -0.01022 -0.58560 48303 48296 7 -18 -11 2.023 pair: 5 20906 20919 -336 -323 43527 43535 155 163 -0.00757 -0.43369 48295 48294 1 -13 -8 5.993 pair: 6 20902 20905 -203 -206 43537 43525 -89 -101 -0.00470 -0.26916 48293 48287 6 3 12 2.981 pair: 7 20900 20897 -140 -137 43539 43544 -68 -63 -0.00318 -0.18225 48298 48296 2 -3 -5 29.997
This quality check works well to catch significant typos in input table. In case of obvious typos input table can be corrected. When the quality check is passed successfully the alignment parameters are saved and deployed under the calib.
Detector geometry model
Since 2014 we support universal detector geometry software which is documented in the Detector Geometry page and in CSPAD-geometry-parameters.pdf.
Alignment parameters from optical measurement
From optical measurement we extract coordinates of the center of each 2x1 sensor and its tilt angle.
The center coordinates are evaluated as an averaged over 4 corners measurements for each axis.
The tilt parameters are used along with rotation to completely define orientation of 2x1 in quad (for CXI) or in detector (for XPP).
Alignment of quads in the detector
For CSPad with fixed quad geometry (like in XPP) optical measurement of entire detector (should) produces complete information for geometry alignment.
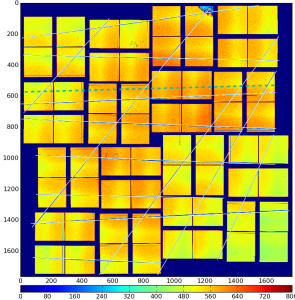
For CSPad with moveable quads (like in CXI) quads relative position needs to be adjusted through the alignment parameters for quads. It is usually done using typical images with diffraction rings, wires or other shading objects:
Although few algorithms of automatic quad alignment were tried, we did not find good generic way for automated quad tuning. Currently, the quad tuning parameters in marg_gap_shift and offset_corr are adjusted manually for runs with specific images.
Calibration store
The official space for CSPAD alignment parameters is
/reg/d/psdm/<INSTRUMENT>/<experiment>/calib/CsPad::Calib<VERSION>/<CSPad-name>/<type>/<run-range>.data
For example:
/reg/d/psdm/CXI/cxi80410/calib/CsPad::CalibV1/CxiDs1.0:Cspad.0/geometry/1142-end.data
The file name consists of the run range followed by the .data extension, for example, 0-end.data, 11-end.data, 47-52.data, etc.
Calibration type
Detector geometry calibration information is located in a single file of type
geometry- contains hierarchical description of all detector components; for example for CSPAD, sensors' location and rotation in the quads, quads - in the detector, detector - in the setup, etc.
Archive and History
Optical measurement and other alignment files can be found in
- /reg/g/psdm/detector/alignment/cspad/
- Geometry History
Detector data access software
References
- CSPAD Geometry and Alignment - Depricated - old version of this page
- Detector Geometry - confluence page
- CSPAD in DAQ - schematic description of CSPAD geometry available in DAQ.
- CSPAD quad metrology - slides for CXI type CSPAD quads
- CSPad pixel layout in quads - pdf file with numeration of ASICs in the CSPAD quads
- XPPMetrologyAnnotated.pdf - order of measurements of XPP camera.
- Geometry History - page with references to calibration files.
- Detector data access software - auto-generated documentation of the Detector package.