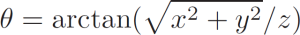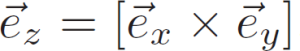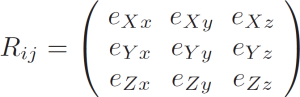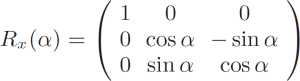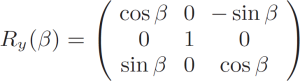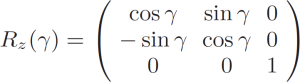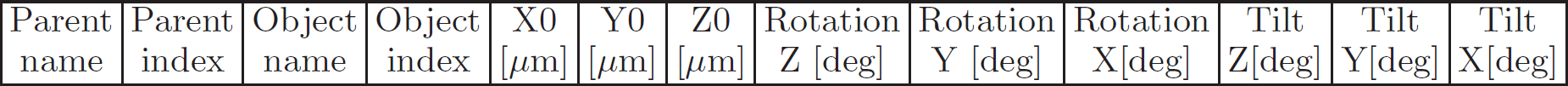This note describes imaging detectors' hierarchical geometry model implemented in LCLS offline software releases since ana-0.13.1.
Content
Introduction
Note that public detector geometry data can be found here.
Nearly all imaging experiments conducted at LCLS require a precise description of the experimental geometry, especially how one or more area detectors are arranged with respect to the x-ray beam and interaction site. In pixel array detectors photon energy is usually deposited in a single pixel and hence a description of the experimental geometry should aim to provide the pixel location to a precision comparable with or better than its size, for the CSPAD about 100μm.
Determination of the experimental geometry to such a precision is a challenging task for many reasons:
- position of the detector sensors relative to interaction point (IP) of the photon beam with target is not well known,
- in some cases detector is a composition of other sub-detectors arranged together and consisting of other sub-detectors and so on,
- sub-detectors of each layer may have stable positions or be moved by stepping motor relative to each other,
- final level sub-detector is represented by precisely engineered sensor(s) of particular type(s) which geometry needs to be tabulated.
To take into account this structure we may consider a variable length series of hierarchical objects like sensor -> sub-detector -> detector -> setup, where lower-level child object(s) is(are) embedded in its higher-level parent object. Nodes/objects of this hierarchical model form the tree which is convenient for navigation and recursion algorithms. Each child object location and orientation can be described in the parent frame. Tree-like structure can be kept in form of table saved in and retrieved from file. The last feature is practically useful for calibration purpose. All constants for detector/experiment geometry description can be saved in a single file. Relevant parts of the hierarchical table can be calibrated and updated whenever new geometry information is available, for example from optical measurement or dedicated runs with images of bright diffraction rings or Bragg peaks.
This note contains description of the implemented hierarchical geometry model, coordinate transformation algorithms, tabulation of the hierarchical objects and calibration file format, description of software interface in C++ and Python, details of calibration, etc.
Coordinate frames
In this section we list tentative objects and associated coordinate frames which may be involved in typical LCLS experimental setup and explain how they can be inscribed in the hierarchical model.
Experimental setup
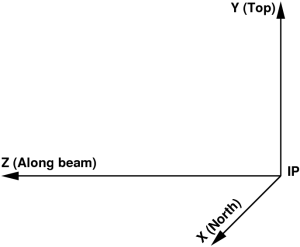
On the very top level of hierarchical structure there should be a global coordinate frame associated with entire experimental setup. All other setup components are defined relative to the global coordinate frame. In diffraction experiments origin of the coordinate frame is usually associated with IP. Choice of axes directions depends on experimental preferences. In some of LCLS experiments Cartesian coordinate system of the setup is defined by the three mutually orthogonal right-hand-indexed axes with origin in the IP:
- X axis pointing from IP to the north,
- Y axis pointing from IP to the top, and
- Z axis pointing from IP along the photon beam propagation direction,
as shown in the plot:
FIG. 1: Tentative coordinate frame of experimental setup.
In this frame photon-hit pixel coordinates (x, y, z) can be easily transformed to the photon diffraction angle θ,
(1)
Sensor
On the very bottom level of hierarchy structure there should be self-sufficient components of the detector - sensors a.k.a. tiles, segments, pixel arrays/matrix etc. We assume that
- tiles may be of different types even in a single detector,
- all tiles of the same type have identical geometry,
- by design each tile has well defined geometry of pixels which does not need in calibration,
- pixel center (x, y, z) coordinates in each tile can be defined as a look-up table for all pixels,
- each tile is represented in data as a minimal solid block of memory,
- “natural” matrix-style pixel numeration is preferable for simplicity of the tile description but is not necessarily required
For example, CSPAD 2x1 tile pixel geometry is schematically shown in Fig.2.
FIG. 2: Coordinate frame of CSPAD 2x1 sensor. Note that a right-handed rule is used for the coordinate system, so the z-axis is coming out of the page. This "native" sensor frame is initially aligned with the global coordinate system; the sensor is then positioned by applying translations and rotations relative to that native frame.
The CSPAD 2x1 tile has
- 185 rows and 388 columns of pixels,
- regular pixel size is 109.92 × 109.92 μm²,
- pixel size in two middle columns (193 and 194) is 274.80 × 109.92 μm².
The pixel index and coordinates in the tile memory block of size 185×388 can be evaluated as
y = k * row + y_offset
x = f(column)
where y coordinate is proportional to the row index, while x coordinate needs to be tabulated as a function of the column index due to the gap in the tile central columns braking matrix uniformity. Detector data record consists of consecutive tile-memory blocks, in accordance with numeration adopted in DAQ. For effective memory management, some of the tile-blocks may be missing due to current detector configuration. Available configuration of the detector tile-blocks should be marked in a configuratiomn bit-mask word in positional order (bit position from lower to higher is associated with the tile number in DAQ).
Child geometry object in the parent frame
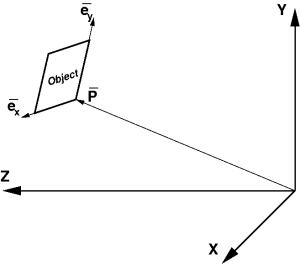
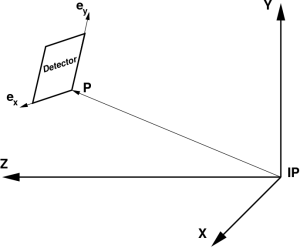
Full description of a composite detector (beside top and bottom level hierarchical objects) needs in definition of intermediate objects with their arbitrary location and orientation. Any geometry object coordinate system may have a translation and rotation with respect to the parent object, which can be defined by the 3 vectors in the setup frame as shown in Figure
FIG. 3: Child object position in the parent coordinate frame.
where
- P is a translation vector pointing from parent to its child frame origin,
- ex is a unit vector along the child frame x axis,
- ey is a unit vector along the child frame y axis.
Third unit vector ez is assumed to be right-hand triplet component, . Components of these three unit vectors form the rotation matrix
(2)
where index “j” enumerates unit vectors in the object coordinate frame, and index “i” is an object unit vector component in the parent frame (ex.: eYz is a Y component of the vector ez). Within this definition 3-d pixel coordinate “c” in the object frame can be transformed to the parent coordinate frame “C” using equation
Ci=Rij·cj + Pi. (3)
For practical reason we parametrize rotation matrix Rij in terms of Cardan’s angles R(α, β, γ). We assume that the 3-d rotation matrix R(α, β, γ) is a product of three 2-d rotations
R(α, β, γ) = Rx(α) · Ry(β) · Rz(γ), (4)
around appropriate axes, defined as
(5)
This transformation algorithm is implemented in class PSCalib.GeometryObject as discussed below.
Example of composite detector
As an example we show how composite CXI-like CSPAD detector with moving quads can be inscribed in the hierarchical geometry model and how geometry parameters can be retrieved in each level.
- CSPAD 2x1 sensor (Fig. 2) is the low-level object with completely specified geometry of pixels.
- A group of eight cspad 2x1 sensors forms a quad (Fig. 4). Sensors’ positions in the quad can be measured by optical microscope.
- Four quads form a CSPAD detector. In CXI-like CSPAD quads can be moved by the stepping motor. For technical reason this detector can not be measured with optical microscope. Dedicated runs with bright images of test wires, diffraction rings, or Bragg peaks can be used to calibrate relative quad positions. Then, quads’ position variation by the stepping motor can be accounted for once calibrated quads.
- Finally, detector position relative to IP should be accounted (Fig. 6). Detector position and orientation can be measured by the ruler in the hatch for the first approximation. The same dedicated runs with bright images can be used to evaluate precise detector coordinates. Calibration runs with a few detector positions along the beam line can be helpful for full geometry parameters reconstruction.
FIG. 4: Example: 2x1 sensors’ positions in the CSPAD quad coordinate frame.
FIG. 5: Example: quads’ positions in the CSPAD detector coordinate frame.
FIG. 6: Example: detector position in the experiment coordinate frame with origin at IP.
Optical measurements
Precise pixel coordinates can be retrieved in a few steps using
- ideal tile design geometry (Fig. 2),
- results of measurements with optical microscope,
- correction of sub-detector elements using dedicated runs.
In this section we describe a procedure of optical measurements, its potential problem, and method to fix it.
Metrology file
Optical measurements with microscope give the most precise information about sensors’ positions in the parent structure. Estimated accuracy of measurements is σRMS ∼ 10μm in x-y plane, and about the same amount in z. Optical measurements provide 3-d coordinates of 4 corners for all tiles in the (sub-)detector in some arbitrary microscope plane which coincides with detector imaging array (tiles) plane within precision of installation.
- Tile corner coordinates do not necessarily coincide with pixel centers or corners.
- Numeration of tiles in optical measurements should not necessarily coincide with their numeration in DAQ, but it should be done in expected order with indication of tile numbers.
- Optical measurements are saved in the xlsx file as a table of x, y, z coordinates for all sensor corners with records like
Tile <#>
Point <#> <X[um]> <Y[um]> <Z[um]>
- Metrology files are produced by the detector group for new or repaired detectors.
Quality check
Measurements with microscope are not automated. Results are manually saved in the metrology file, which may have non-intentional typos. If the number of typos is small they can be tracked down in the quality check and fixed. Quality check of optical measurement may test for each tile:
- equity of opposite sides
- equity of diagonals
- equity of tilt angles for all sides
- tile flatness in 3-d
Report table about all deviations is generated by the python script processing the metrology file. Large deviations exceeding standard precision >3σ(RMS) indicate on problem with measurement. A few corrections are usually applied for each metrology file.
Calibration file
In this section we discuss requirements to the geometry alignment parameters and describe chosen file format.
Hierarchical structure
In the calibration file/table we need to save links between parent and child objects. Tree-like structure assumes that each parental object may have many children and each child object has only one parent. It is easier for each object to keep information about its parent and object location and orientation parameters with respect to the parent, as implemented in class PSCalib.GeometryObject. One fixed length record per object is convenient to keep this information in memory and file as a table. Scan over all objects allows to retrieve all hierarchical links and use them further in recursive processing. This algorithm is implemented in the class PSCalib.GeometryAccess.
Object identification
Composite detector usually consists of similar sub-detectors. In particular, CSPAD consists of four quads, quad consists of eight 2x1 sensors. Sub-detectors of the same type should be treated by the same code. To distinguish between sub-detectors we introduce two variable for each object, name and index. For example, CSPAD quads have an arbitrary symbolic name “QUAD” and indexes from 0 to 3, their children have a symbolic name “CSPAD2X1V1” and indexes from 0 to 7. The name of low level objects, “CSPAD2X1V1”, is used in the factory method PSCalib.SegGeometryStore.Create in order to instantiate associated PSCalib.SegGeometry object. This and all other names are also used to set child-parent relations between objects.
Assumptions about detector geometry
In most cases we deal with planar detectors and we assume that:
- the detector image is produced by a set of tiles,
- all tiles form almost flat (x-y) surface around z=0 within precision of production technology and installation,
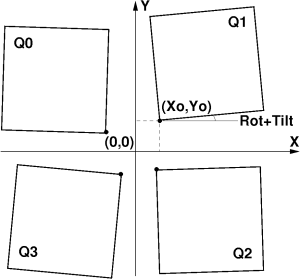
- the tile rotation angles in (x-y) are N*90 degrees, where N=0,1,2,or 3, detector local coordinate system is defined
in this plane, as explained below. These assumptions are not necessary for all algorithms. But, in many cases it may be convenient to use small angle approximation or ignore angular misalignment for image mapping between tiles and 2-d image array. For this reason in calibration file we split all angles for rotation and tilt in order to have direct access to the designed and corrected values, respectively.
File format
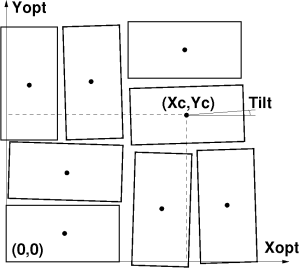
From metrology file we may evaluate the tile center coordinates as an average over 4 corners. Tilt angles are defined as projected angles of the tile sides on relevant planes. Each angle is evaluated as an averaged angle for 2 sides. The tile location and orientation in the parent frame can be saved in the table record where
- Parent name - name and version of the parent object; all translation and rotation pars are defined w.r.t. parent Cartesian frame
- Parent index - index of the parent object
- Object name - name and version of the object inserted in the parent frame
- Object index - index of the object
- X0, Y0, and Z0 [μm] - object frame origin coordinates in the parent frame
- Rotation X, Y, and Z [degree] - object ideal (design) rotation angle around X, Y, and Z axis of the parent frame, respectively,
- Tilt X, Y, and Z [degree] - tilt angles for correction of the object rotation angles around X, Y, and Z axis of the parent frame, respectively.
First four fields are intended to set parent-to-child relations between geometry objects. Python script in CalibManager reads data from the metrology file and generates the geometry file consisting of records in this format. Thus tabulated geometry parameters allow to
- accommodate parameters from optical measurement,
- update information about sub-detectors later,
- retrieve all hierarchical links.
Result of multiple geometry transformations depends on their order. In coordinate reconstruction algorithms we use particular order for rotations and translations.
Calibration file example
CalibManager under the tabs Geometry / Metrology has a GUI which processes metrology file and generates the calibration file like shown below for CXI-like CSPAD with moving quads
# TITLE Geometry parameters of CSPAD-CXI # DATE_TIME 2014-10-03 12:20:44 PDT # METROLOGY /reg/neh/home1/dubrovin/LCLS/CSPadMetrologyProc/2014-05-15-CSPAD-CXI-DS1-Metrology-corr.txt # AUTHOR dubrovin # EXPERIMENT Any # DETECTOR CSPAD-CXI # CALIB_TYPE geometry # COMMENT:01 Table contains the list of geometry parameters for alignment of 2x1 sensors, quads, CSPAD, etc # COMMENT:02 All translation and rotation pars of the object are defined w.r.t. parent object Cartesian frame # PARAM:01 PARENT - name and version of the parent object # PARAM:02 PARENT_IND - index of the parent object # PARAM:03 OBJECT - name and version of the object # PARAM:04 OBJECT_IND - index of the new object # PARAM:05 X0 - x-coordinate [um] of the object origin in the parent frame # PARAM:06 Y0 - y-coordinate [um] of the object origin in the parent frame # PARAM:07 Z0 - z-coordinate [um] of the object origin in the parent frame # PARAM:08 ROT_Z - object design rotation angle [deg] around Z axis of the parent frame # PARAM:09 ROT_Y - object design rotation angle [deg] around Y axis of the parent frame # PARAM:10 ROT_X - object design rotation angle [deg] around X axis of the parent frame # PARAM:11 TILT_Z - object tilt angle [deg] around Z axis of the parent frame # PARAM:12 TILT_Y - object tilt angle [deg] around Y axis of the parent frame # PARAM:13 TILT_X - object tilt angle [deg] around X axis of the parent frame # HDR PARENT IND OBJECT IND X0[um] Y0[um] Z0[um] ROT-Z ROT-Y ROT-X TILT-Z TILT-Y TILT-X QUAD:V1 0 SENS2X1:V1 0 21757 33110 51 0 0 0 0.04474 -0.14079 -0.00274 QUAD:V1 0 SENS2X1:V1 1 21769 10457 18 0 0 0 0.01053 -0.11974 0.00000 QUAD:V1 0 SENS2X1:V1 2 33464 68275 -28 270 0 0 -0.01645 0.10414 0.09737 QUAD:V1 0 SENS2X1:V1 3 10769 68299 18 270 0 0 -0.02828 0.02740 0.13418 QUAD:V1 0 SENS2X1:V1 4 68489 56732 71 180 0 0 -0.05128 -0.11309 0.06303 QUAD:V1 0 SENS2X1:V1 5 68561 79628 -20 180 0 0 -0.03552 0.07104 -0.11788 QUAD:V1 0 SENS2X1:V1 6 77637 21754 -15 270 0 0 -0.33657 -0.00821 0.01183 QUAD:V1 0 SENS2X1:V1 7 54810 21558 -54 270 0 0 -0.06315 0.00000 0.00658 QUAD:V1 1 SENS2X1:V1 0 21757 33329 178 0 0 0 0.08883 0.03158 -0.20830 QUAD:V1 1 SENS2X1:V1 1 21773 10446 61 0 0 0 -0.01448 0.04211 -0.24943 QUAD:V1 1 SENS2X1:V1 2 33430 68158 257 270 0 0 0.02698 -0.04660 -0.07370 QUAD:V1 1 SENS2X1:V1 3 10628 68183 247 270 0 0 0.04014 -0.08498 -0.06448 QUAD:V1 1 SENS2X1:V1 4 68349 56949 161 180 0 0 -0.00066 -0.02895 0.05481 QUAD:V1 1 SENS2X1:V1 5 68345 79783 231 180 0 0 0.06843 -0.13948 0.03836 QUAD:V1 1 SENS2X1:V1 6 77454 21811 111 270 0 0 0.05919 -0.06029 -0.11707 QUAD:V1 1 SENS2X1:V1 7 54729 21779 106 270 0 0 0.07632 -0.04933 -0.16580 QUAD:V1 2 SENS2X1:V1 0 21741 33265 0 0 0 0 -0.06053 0.00000 0.00000 QUAD:V1 2 SENS2X1:V1 1 21752 10493 0 0 0 0 0.10132 0.00000 0.00000 QUAD:V1 2 SENS2X1:V1 2 32869 68638 0 270 0 0 0.07036 0.00000 0.00000 QUAD:V1 2 SENS2X1:V1 3 10462 68624 0 270 0 0 0.00658 0.00000 0.00000 QUAD:V1 2 SENS2X1:V1 4 68166 57261 0 180 0 0 0.17894 0.00000 0.00000 QUAD:V1 2 SENS2X1:V1 5 68109 79832 0 180 0 0 0.11972 0.00000 0.00000 QUAD:V1 2 SENS2X1:V1 6 77482 21698 0 270 0 0 -0.02762 0.00000 0.00000 QUAD:V1 2 SENS2X1:V1 7 54709 21779 0 270 0 0 0.02499 0.00000 0.00000 QUAD:V1 3 SENS2X1:V1 0 21730 33098 102 0 0 0 0.09278 -0.05132 -0.27140 QUAD:V1 3 SENS2X1:V1 1 21755 10477 40 0 0 0 0.06580 -0.02369 -0.32612 QUAD:V1 3 SENS2X1:V1 2 33193 68452 272 270 0 0 0.34083 -0.02192 -0.18687 QUAD:V1 3 SENS2X1:V1 3 10904 68416 270 270 0 0 0.01645 0.00823 -0.15397 QUAD:V1 3 SENS2X1:V1 4 68570 56923 194 180 0 0 0.12435 0.06974 0.07401 QUAD:V1 3 SENS2X1:V1 5 68456 79666 246 180 0 0 0.20857 0.04737 0.12882 QUAD:V1 3 SENS2X1:V1 6 77425 21681 60 270 0 0 0.05264 0.00274 -0.30004 QUAD:V1 3 SENS2X1:V1 7 54648 21761 118 270 0 0 0.01645 -0.00822 -0.22107 CSPAD:V1 0 QUAD:V1 0 -4500 -4500 0 90 0 0 0.00000 0.00000 0.00000 CSPAD:V1 0 QUAD:V1 1 -4500 4500 0 0 0 0 0.00000 0.00000 0.00000 CSPAD:V1 0 QUAD:V1 2 4500 4500 0 270 0 0 0.00000 0.00000 0.00000 CSPAD:V1 0 QUAD:V1 3 4500 -4500 0 180 0 0 0.00000 0.00000 0.00000
All lines started with hash “#” are comments, which are also accessible through the program interface as a dictionary. XPP-like CSPAD with all sensors attached to the same plate is measured as a single detector. Its content part omits quads
# TITLE Geometry parameters of CSPAD-XPP # METROLOGY /reg/neh/home1/dubrovin/LCLS/CSPadMetrologyProc/2013-10-09-CSPAD-XPP-Metrology.txt ... # HDR PARENT IND OBJECT IND X0[um] Y0[um] Z0[um] ROT-Z ROT-Y ROT-X TILT-Z TILT-Y TILT-X CSPAD:V2 0 SENS2X1:V1 0 51621 112683 153 90 0 0 0.48292 0.00000 0.00263 CSPAD:V2 0 SENS2X1:V1 1 74168 112907 135 90 0 0 0.48886 -0.05755 0.01316 CSPAD:V2 0 SENS2X1:V1 2 16366 124137 107 0 0 0 0.32370 0.00395 -0.01096 CSPAD:V2 0 SENS2X1:V1 3 16415 101350 185 0 0 0 0.15130 0.09867 -0.29055 CSPAD:V2 0 SENS2X1:V1 4 27786 159233 123 270 0 0 0.24474 -0.03015 0.03948 CSPAD:V2 0 SENS2X1:V1 5 4845 159260 106 270 0 0 0.05987 -0.04659 0.01053 CSPAD:V2 0 SENS2X1:V1 6 62758 168631 132 0 0 0 0.44940 0.02895 -0.00548 CSPAD:V2 0 SENS2X1:V1 7 62881 145851 137 0 0 0 0.20068 0.03553 -0.03015 CSPAD:V2 0 SENS2X1:V1 8 107098 129494 165 0 0 0 0.01316 0.01184 -0.02742 CSPAD:V2 0 SENS2X1:V1 9 107067 106699 152 0 0 0 -0.15924 -0.01316 -0.05208 CSPAD:V2 0 SENS2X1:V1 10 118871 164660 152 270 0 0 0.11249 -0.02193 0.04078 CSPAD:V2 0 SENS2X1:V1 11 95879 164632 143 270 0 0 -0.07632 -0.05757 0.03158 CSPAD:V2 0 SENS2X1:V1 12 153905 153051 158 180 0 0 -0.03026 0.00000 -0.04385 CSPAD:V2 0 SENS2X1:V1 13 153838 175841 140 180 0 0 -0.03947 -0.01973 -0.16719 CSPAD:V2 0 SENS2X1:V1 14 163149 117980 156 270 0 0 -0.17500 -0.04385 -0.00526 CSPAD:V2 0 SENS2X1:V1 15 140287 117936 153 270 0 0 0.00000 -0.02741 -0.00790 CSPAD:V2 0 SENS2X1:V1 16 123905 73726 133 270 0 0 0.00263 -0.00548 -0.00921 CSPAD:V2 0 SENS2X1:V1 17 101282 73699 130 270 0 0 0.20725 -0.02740 -0.03948 CSPAD:V2 0 SENS2X1:V1 18 159023 62203 142 180 0 0 -0.05461 -0.00263 -0.03562 CSPAD:V2 0 SENS2X1:V1 19 159024 84885 136 180 0 0 -0.08026 0.01579 -0.06576 CSPAD:V2 0 SENS2X1:V1 20 147998 26847 106 90 0 0 0.03158 -0.08219 0.08947 CSPAD:V2 0 SENS2X1:V1 21 170404 26856 96 90 0 0 -0.07893 -0.00822 0.06972 CSPAD:V2 0 SENS2X1:V1 22 112701 17748 97 180 0 0 0.26908 -0.02500 -0.00548 CSPAD:V2 0 SENS2X1:V1 23 112640 40586 100 180 0 0 0.03685 -0.01448 0.03836 CSPAD:V2 0 SENS2X1:V1 24 68448 57015 119 180 0 0 0.27835 -0.02501 0.09319 CSPAD:V2 0 SENS2X1:V1 25 68292 79701 120 180 0 0 0.37440 -0.03290 -0.04112 CSPAD:V2 0 SENS2X1:V1 26 56919 21965 69 90 0 0 0.18024 -0.06578 0.07894 CSPAD:V2 0 SENS2X1:V1 27 79497 22002 67 90 0 0 0.12040 -0.02740 0.09211 CSPAD:V2 0 SENS2X1:V1 28 21658 33119 72 0 0 0 0.27240 0.03553 -0.12332 CSPAD:V2 0 SENS2X1:V1 29 21748 10489 28 0 0 0 0.09805 0.03027 -0.07946 CSPAD:V2 0 SENS2X1:V1 30 12357 68156 97 90 0 0 0.20919 0.03562 0.05789 CSPAD:V2 0 SENS2X1:V1 31 35247 68250 89 90 0 0 0.09144 -0.04109 0.02368
Content of CSPAD2x2 geometry file consist of data for two sensors only:
# TITLE Geometry parameters of CSPAD2X2 # METROLOGY /reg/neh/home1/dubrovin/LCLS/CSPad2x2Metrology/CSPad2x2/2014-04-25-CSPAD2X2-3-MEC-Metrology.txt ... # HDR PARENT IND OBJECT IND X0[um] Y0[um] Z0[um] ROT-Z ROT-Y ROT-X TILT-Z TILT-Y TILT-X CSPAD2X1:V1 0 SENS2X1:V1 0 21848 10490 6 180 0 0 -0.00197 -0.01049 0.03004 CSPAD2X1:V1 0 SENS2X1:V1 1 21943 33908 4 180 0 0 -0.16127 -0.00262 -0.01639
If the detector pixel coordinates should be presented relative to IP or other setup component, have an offset or flipped around axis one more line must to be added, for example
# HDR PARENT IND OBJECT IND X0[um] Y0[um] Z0[um] ROT-Z ROT-Y ROT-X TILT-Z TILT-Y TILT-X SETUP-IP 0 CSPAD2X2:V1 0 -100 200 1000000 0 180 0 0 0 0
Interface implementation
Program interface to the detector geometry parameters consists of a few modules with the same names up to extensions for C++ and Python in the PSCalib package. Sensor geometry:
- PSCalib.SegGeometry - abstract interface for sensor pixels geometry description.
- PSCalib.SegGeometryCspad2x1V1 - implementation of interface for CSPAD 2x1 sensor of version V1.
- PSCalib.SegGeometryStore - static factory method for all available sensor geometry descriptors.
Hierarchical model:
- PSCalib.GeometryObject - class to support one object/node in hierarchical structure.
- PSCalib.GeometryAccess - class to support hierarchical structure and access to the geometry parameters.
C++ program interface description with examples is available in Doxygen documentation. Below we consider Python interface only.
Access to sensor geometry information
Generic program interface to the sensors’ ideal geometry is presented by the abstract class PSCalib.SegGeometry. It declares methods returning number of pixels, rows, columns, pixel size, area, center coordinates relative to sensor coordinate frame, as listed below.
def print_seg_info(self, pbits=0) : """ Prints segment info for selected bits""" def size(self) : """ Returns segment size - total number of pixels in segment""" def rows(self) : """ Returns number of rows in segment""" def cols(self) : """ Returns number of cols in segment""" def shape(self) : """ Returns shape of the segment [rows, cols]""" def pixel_scale_size(self) : """ Returns pixel size in um for indexing""" def pixel_area_array(self) : """ Returns array of pixel relative areas of shape=[rows, cols]""" def pixel_size_array(self, axis) : """ Returns array of pixel size in um for AXIS""" def pixel_coord_array(self, axis) : """ Returns pointer to the array of segment pixel coordinates in um for AXIS""" def pixel_coord_min(self, axis) : """ Returns minimal value in the array of segment pixel coordinates in um for AXIS""" def pixel_coord_max(self, axis) : """ Returns maximal value in the array of segment pixel coordinates in um for AXIS""" def pixel_mask_array(self, mbits) : """ Returns array of masked pixels which content depends on bontrol bitword mbits"""
Currently this abstract interface has the only implementation for CSPAD2x1 in the class PSCalib.SegGeometryCspad2x1V1. Other versions of CSPAD2x1, ePix, pnccd, etc. sensors can be added later. Static factory method Create in class PSCalib.SegGeometryStore allows to access any sensor geometry information by the detector independent way. For example, pixel x-, y-, and z-coordinate arrays can be directly retrieved from class PSCalib.SegGeometryCspad2x1V1:
from PSCalib.SegGeometryCspad2x1V1 import cspad2x1_one xarr, yarr, zarr = cspad2x1_one.pixel_coord_array()
or using generic access method through the factory method:
from PSCalib.SegGeometryStore import sgs sg = sgs.Create(’SENS2X1:V1’, pbits=0377) xarr, yarr, zarr = sg.pixel_coord_array()
return the same x-, y-, and z-coordinate arrays of shape=[185,388].
This interface is used internally in the geometry service modules and, until it is absolutely necessary, should not be used directly. Doxygen/Sphinx documentation for C++/Python modules is available in References.
Pixel coordinates transformation
Child geometry object pixel coordinates are transformed to the parent frame pixel coordinates in accordance with Eqn 3. We use rotation matrix expressed in terms of cosines and sines of rotation angles as shown in Eqs. 4-5 First we apply rotations around z, y, and x axes then translation. Note, that order of operations is important. This transformation algorithm is implemented in the class PSCalib.GeometryObject. For example, in Python module PSCalib.GeometryObject.py all transformations of pixel coordinate arrays are presented by the code
#file: pyimgalgos/src/GeometryObject.py
def rotation(X, Y, C, S) :
Xrot = X*C - Y*S
Yrot = Y*C + X*S
return Xrot, Yrot
class GeometryObject :
...
def transform_geo_coord_arrays(self, X, Y, Z) :
...
# define Cx, Cy, Cz, Sx, Sy, Sz - cosines and sines of rotation + tilt angles
...
X1, Y1 = rotation(X, Y, Cz, Sz)
Z2, X2 = rotation(Z, X1, Cy, Sy)
Y3, Z3 = rotation(Y1, Z2, Cx, Sx)
Zt = Z3 + self.z0
Yt = Y3 + self.y0
Xt = X2 + self.x0
return Xt, Yt, Zt
Detector geometry access interface
Public methods of the class PSCalib.GeometryAccess:
def __init__(self, path, pbits=0) :
"""Constructor of the class"""
def get_pixel_coords(self, oname=None, oindex=0) :
"""Returns three pixel X,Y,Z coordinate arrays for top or specified geometry object"""
def get_pixel_areas(self, oname=None, oindex=0) :
"""Returns pixel areas array for top or specified geometry object"""
def get_pixel_mask(self, oname=None, oindex=0, mbits=0377) :
"""Returns pixel mask array for top or specified geometry object.
mbits =+1 - mask edges
+2 - two wide-pixel central columns
+4 - non-bounded pixels
+8 - neighbours of non-bounded pixels"""
def get_pixel_scale_size(self, oname=None, oindex=0) :
"""Returns pixel scale size for top or specified geometry object"""
def get_dict_of_comments(self) :
"""Returns dictionary of comments"""
def set_geo_pars(self, oname=None, oindex=0, x0=0, y0=0, z0=0, rot_z=0, rot_y=0, rot_x=0, tilt_z=0, tilt_y=0, tilt_x=0) :
"""Sets geometry parameters for specified or top geometry object"""
def move_geo(self, oname=None, oindex=0, dx=0, dy=0, dz=0) :
"""Moves specified or top geometry object by dx, dy, dz"""
def tilt_geo(self, oname=None, oindex=0, dt_x=0, dt_y=0, dt_z=0) :
"""Tilts specified or top geometry object by dt_x, dt_y, dt_z"""
def print_list_of_geos(self) :
def print_list_of_geos_children(self) :
def print_comments_from_dict(self) :
def print_pixel_coords(self, oname=None, oindex=0) :
"""Partial print of pixel coordinate X,Y,Z arrays for selected or top(by default) geo"""
def get_pixel_coord_indexes(self, oname=None, oindex=0, pix_scale_size_um=None, xy0_off_pix=None) :
"""Returns three pixel X,Y,Z coordinate index arrays for top or specified geometry object"""
def set_print_bits(self, pbits=0) :
""" Sets printout control bitword"""
def set_print_bits(self, pbits=0) :
""" Sets printout control bitword"""
def get_psf(self) :
"""Returns array of vectors in TJ format (psf stands for position-slow-fast vectors)"""
def print_psf(self) :
""" Gets and prints psf array for test purpose"""
# private methods, which may be useful:
def get_geo(self, oname, oindex) :
"""Returns specified geometry object"""
def get_top_geo(self) :
"""Returns top geometry object"""
# global method:
def img_from_pixel_arrays(iX, iY, W=None, dtype=np.float32) :
"""Returns image from iX, iY coordinate index arrays and associated weights W"""
For example:
from PSCalib.GeometryAccess import * fname_geometry = ’<path>/geometry/0-end.data’ geometry = GeometryAccess(fname_geometry, 0377) pix_size = geometry.get_pixel_scale_size() X, Y, Z = geometry.get_pixel_coords(’QUAD:V1’, 1) # for quad X, Y, Z = geometry.get_pixel_coords() # for top object (CSPAD) iX, iY = geometry.get_pixel_coord_indexes(’QUAD:V1’, 1, pix_scale_size_um=None, xy0_off_pix=None) # for quad iX, iY = geometry.get_pixel_coord_indexes(xy0_off_pix=(1000, 1000)) # for top object (CSPAD) img = img_from_pixel_arrays(iX,iY,W=<intensity-array>) img = img_from_pixel_arrays(iX,iY) # Image of 0/1 for fake/real pixels arr = geometry.get_pixel_mask(’QUAD:V1’, 1, 1+2+4+8) arr.shape = (8,185,388) dict_comm = geometry.get_dict_of_comments() d = geometry.get_dict_of_comments() print "d[’DATE_TIME’] = %s" % d[’DATE_TIME’]
Geometry File Format Conversion
crystfel/cheetah/psana
Mikhail Dubrovin has created geometry-conversion scripts. Documentation can be found here: Geometry converter between psana and CrystFEL.
TJ Lane has created geometry-conversion scripts. These were originally in github (https://github.com/LinacCoherentLightSource/psgeom) but have been moved into psana. The methods can be accessed in python but an easier to use wrapper script called "geoconv" has been created. Use "geoconv --help" to see the current syntax.
cctbx/psana
Cctbx.xfel conversion instruction can be found here: http://viper.lbl.gov/cctbx.xfel/index.php/Cxi02416_calibration. Use the following command to convert cbf to psana format:
cxi.cbfheader2slaccalib
There's a command to go from psana format to cctbx, it's not documented above but Aaron Brewster says it is
cxi.slaccalib2cbfheader
Summary
Pixel detector geometry generic parameterization presented in this note is implemented in LCLS analysis software releases since ana-0.13.N. Both C++ and Python interfaces are available.
References
- geometry.pdf - this note in PDF format
- Euler angles, Tait–Bryan angles, nautical angles, Cardan angles etc.
- Autogenerated docs - API description for C++ and Python code
- Python API:
- PSCalib.SegGeometry - abstract interface for sensor pixels geometry description.
- PSCalib.SegGeometryCspad2x1V1 - implementation of interface for CSPAD 2x1 sensor of version V1.
- PSCalib.SegGeometryStore - static factory method for all available sensor geometry descriptors.
- PSCalib.GeometryObject - class to support one object/node in hierarchical structure.
- PSCalib.GeometryAccess - class to support hierarchical structure and access to the geometry parameters.
- LAMP_User_Manual.pdf (useful for determining geometry orientation associated with pnCCD readout order (see table 3))
- Detector alignment tool
- Calibration Management Tool