...
Links:
Data set:
Data set:
-P8R2_SOURCE_V6 80 months of data (MET 239557417 - 444440679)
-Energy: 50 GeV - 2 TeV and 10 GeV - 2 TeV
-Catalog version of 2FHL catalog FSSC version for the 3FHL catalog /u/gl/majello/ki06/P8_10GeV_80m/10GeV/cat_v2.fits
-Data cuts (note the lack of rocking angle cut):
gtselect zmax=105
gtmktime 'IN_SAA!=T&&DATA_QUAL==1&&LAT_CONFIG==1' and roicut=no
gtltcube zmax=105
-Location of the cleaned data (used for the paper) :
FT1 = /u/gl/majello/ki06/P8_10GeV_80m/Filtered/ft1-50GeV_p8_NOrockCut.fits
FT2 = /u/gl/majello/ki06/P8_10GeV_80m/P810GeV_80months-ft2-30s.fits
- LTCUBE: = /u/gl/majello/ki06/P8_10GeV_80m/ltcube_80m_Source_noRock_cut.fits
Surface Brightness Profile (Mattia and Marco)
SOURCE SAMPLES
We have considered the 2FHL and the 3FHL catalog and we have created three different samples of sources.
| E>50 GeV | E>10 GeV |
|---|---|---|
Low z | all z<0.15 |b|>15 (39) | BL Lacs z<0.15 |b|>20 (43) |
High z | all z>0.4 |b|>15 (27) | BL Lacs z>0.70 |b|>20 (43) |
All | all with |b|>20 (198) | BL Lacs with |b|>20 (90) |
The three cases are labelled as "Low z", "High z" and "All" and the number of sources in each sample is reported in parenthesis.
2FHL: We have always considered all AGN and the most of them are BL Lacs
3FHL: We have considered only BL Lacs.
Therefore our catalog of sources is largely given by BL Lacs.
METHOD
Given the above listed samples we have simulated the Galactic diffuse gamma-ray emission, the isotropic diffuse and the emission from the selected sources.
Figure: From left to right panel: Galactic diffuse emission, point sources and the merge of these maps.
For each sample we have performed 30 simulations and the result is averaged on them.
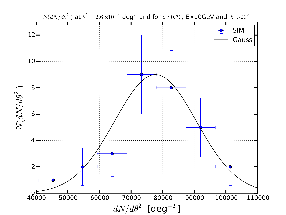
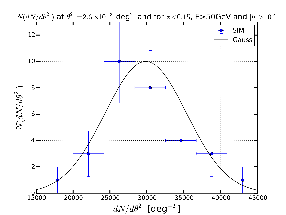
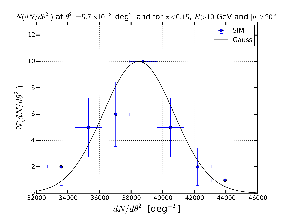
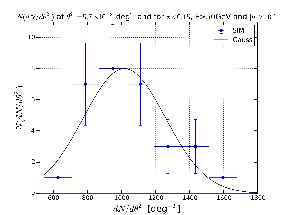
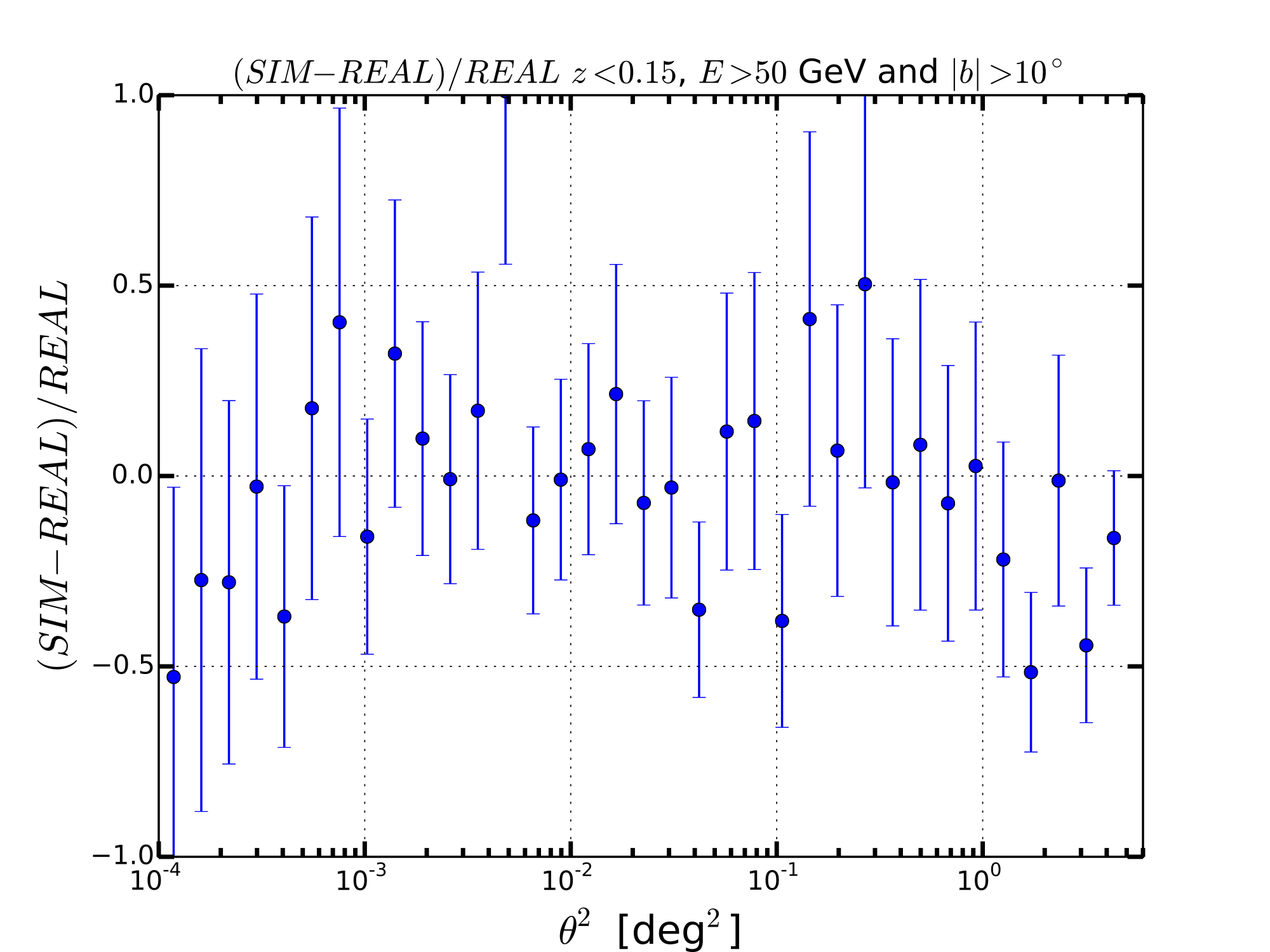
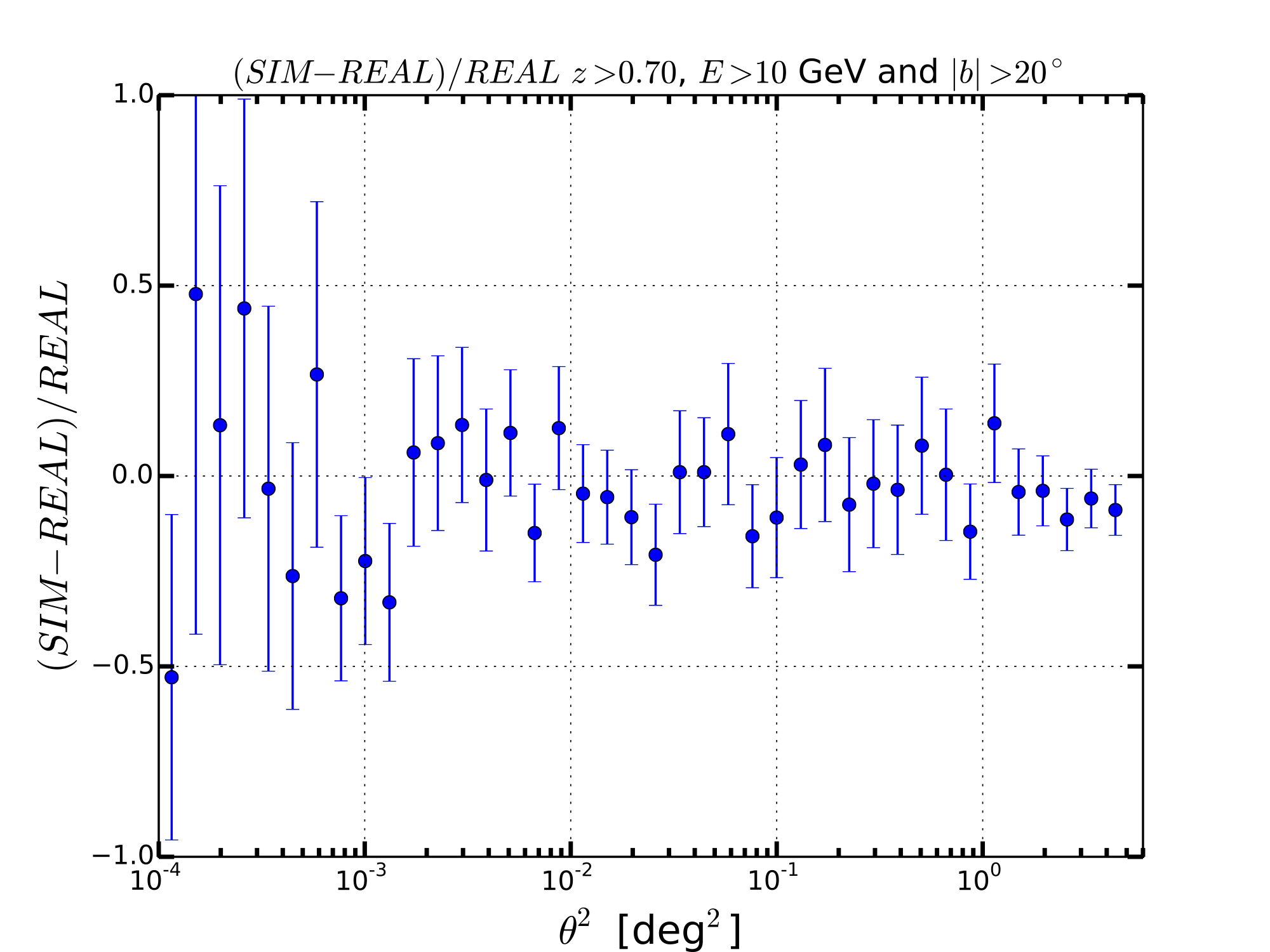
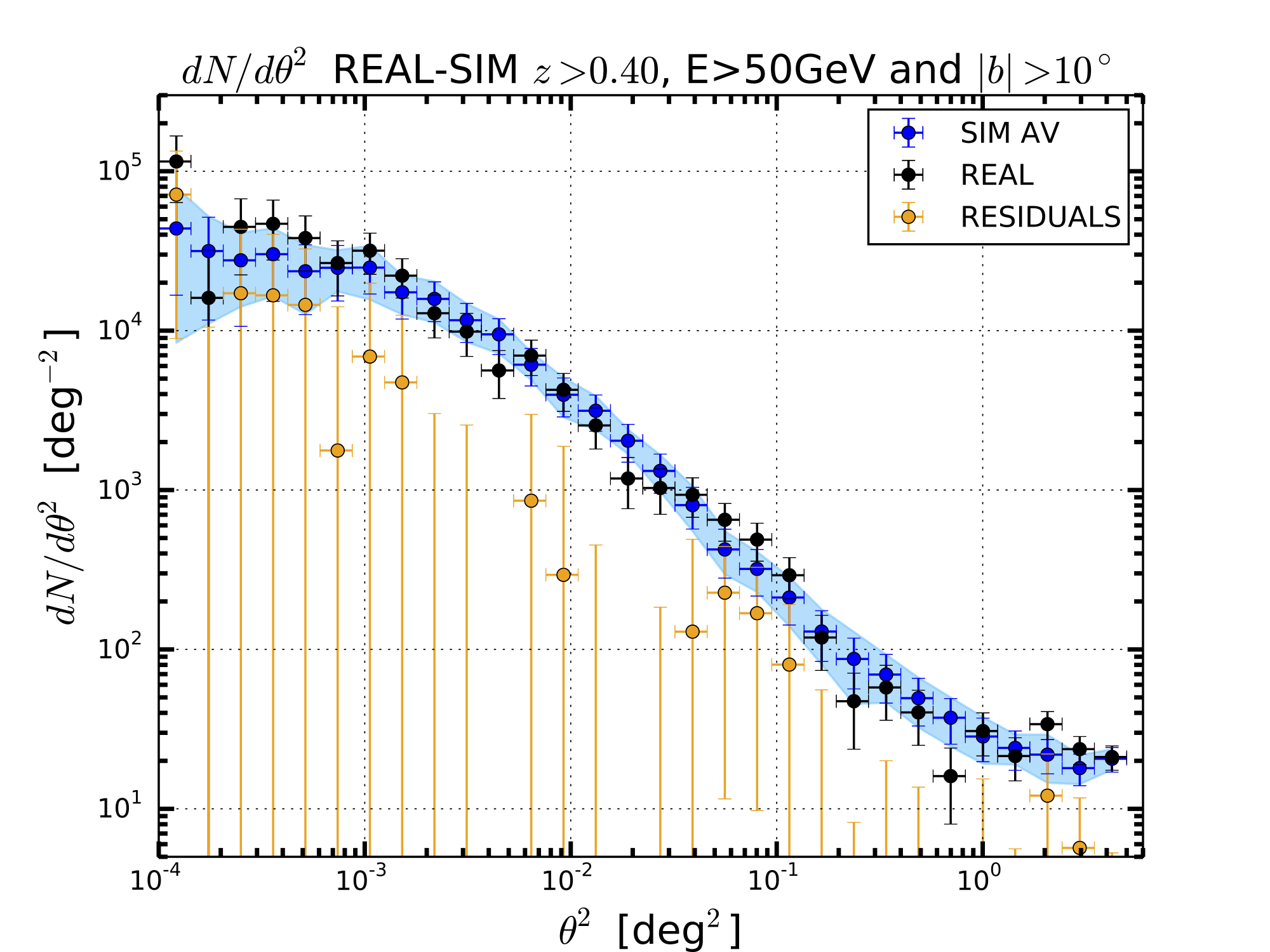
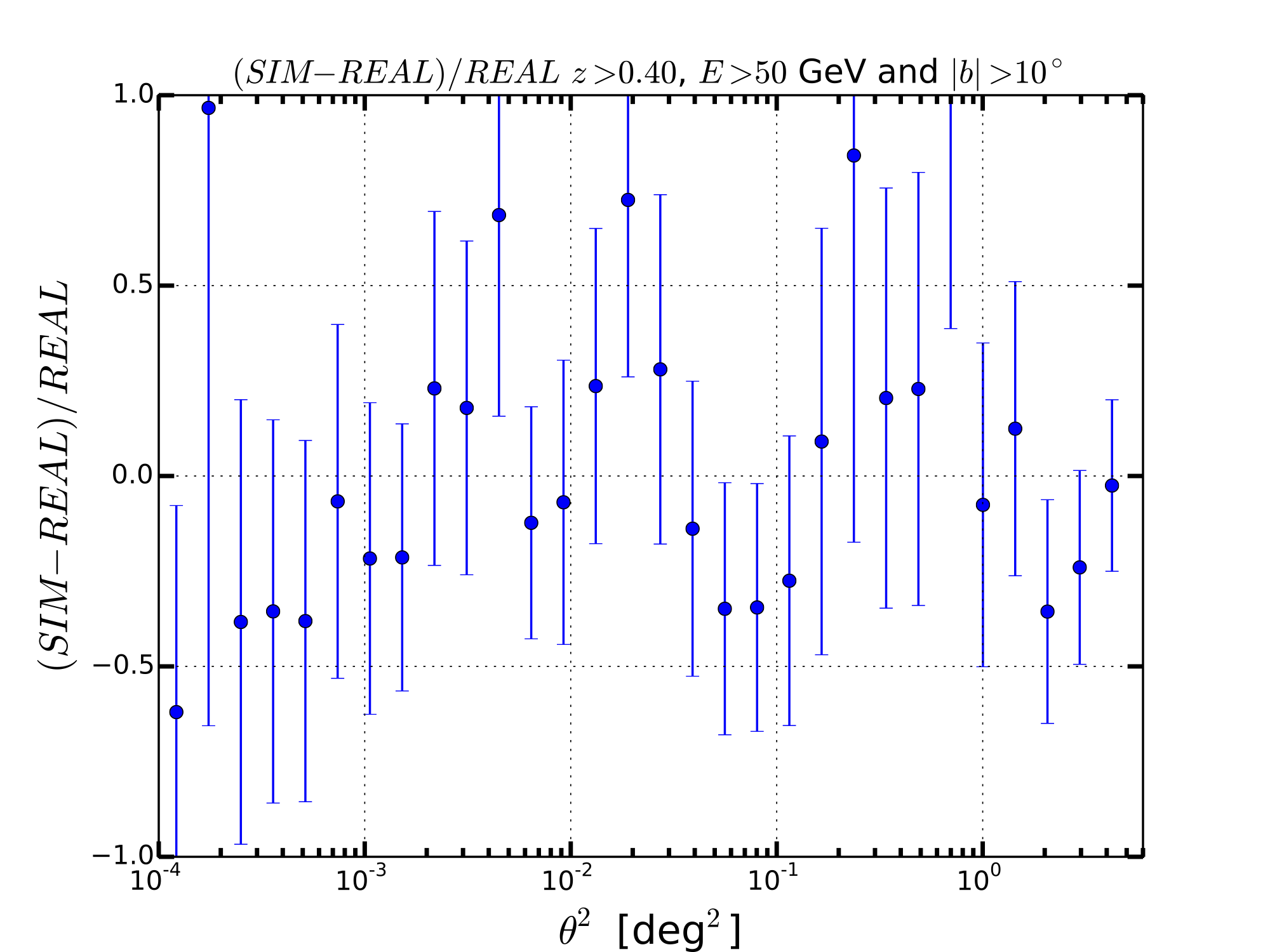
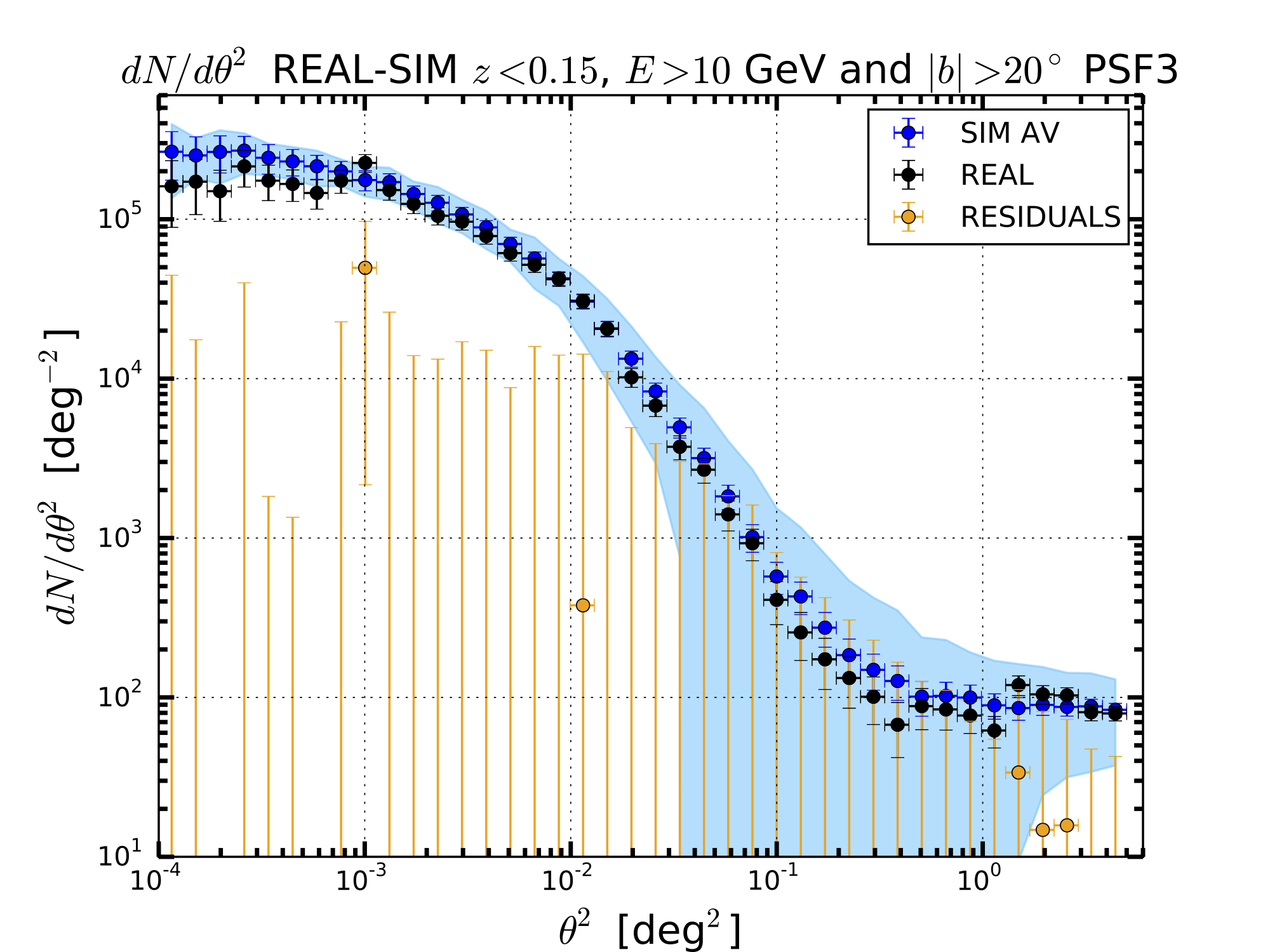
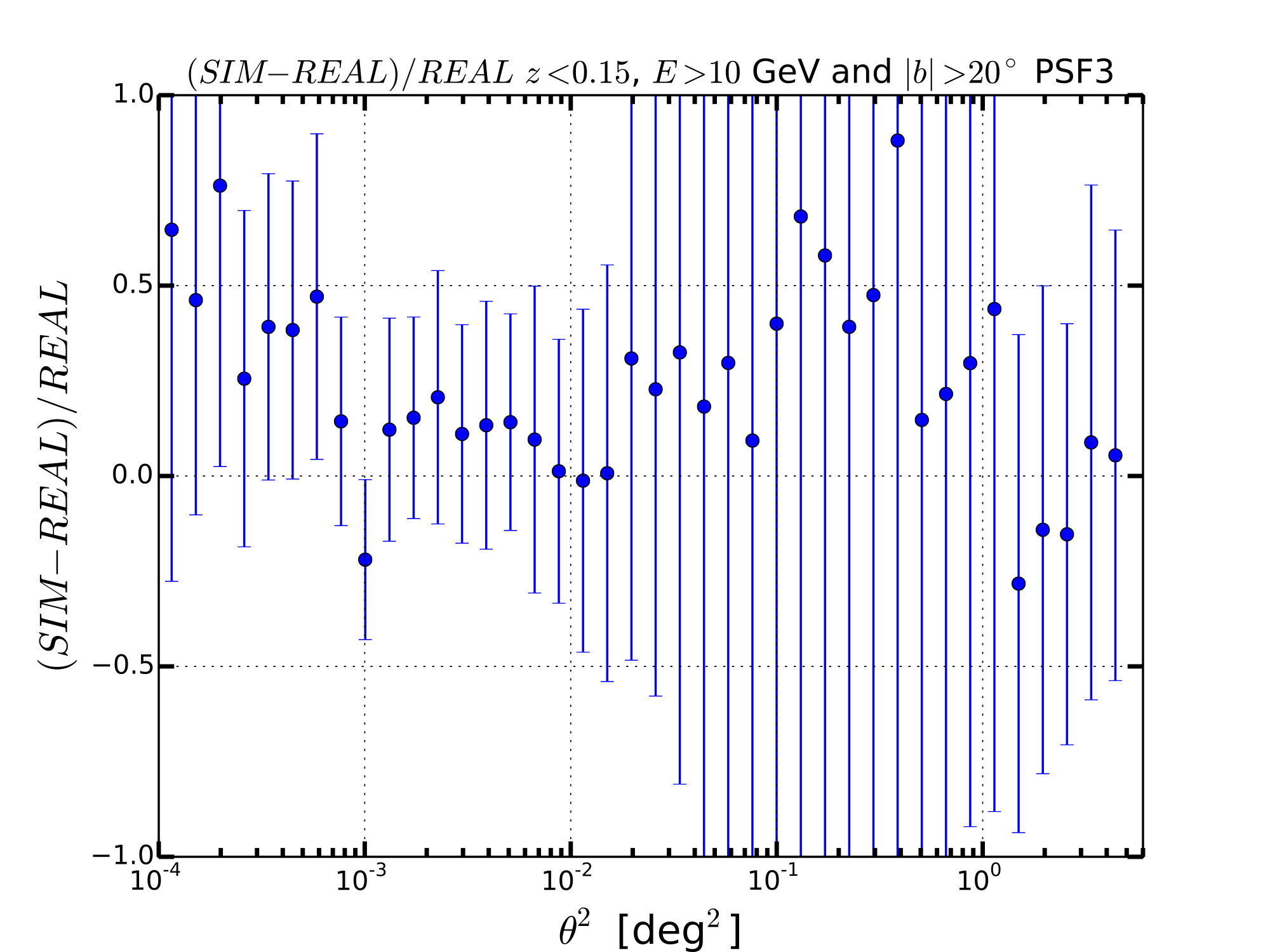
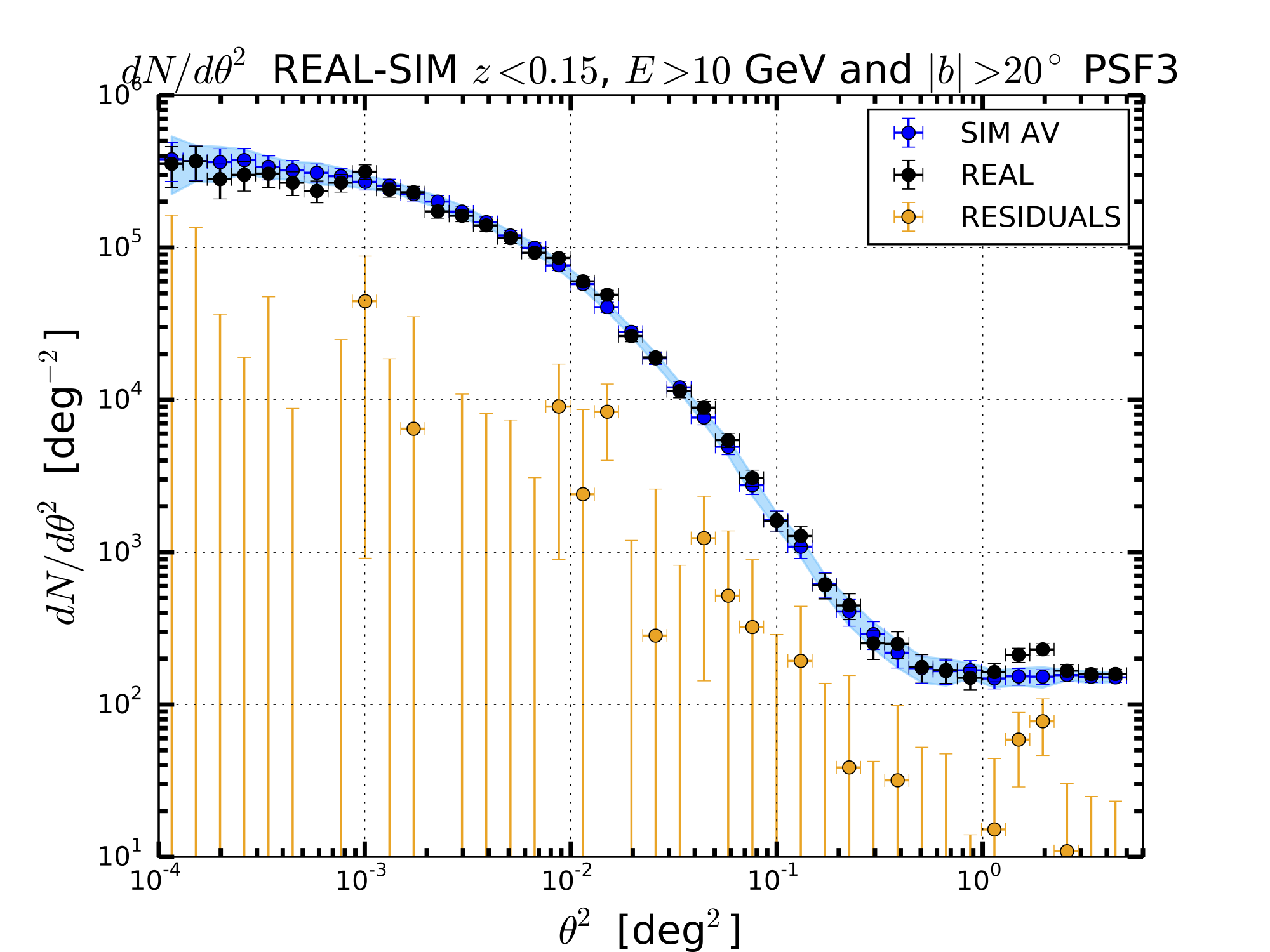
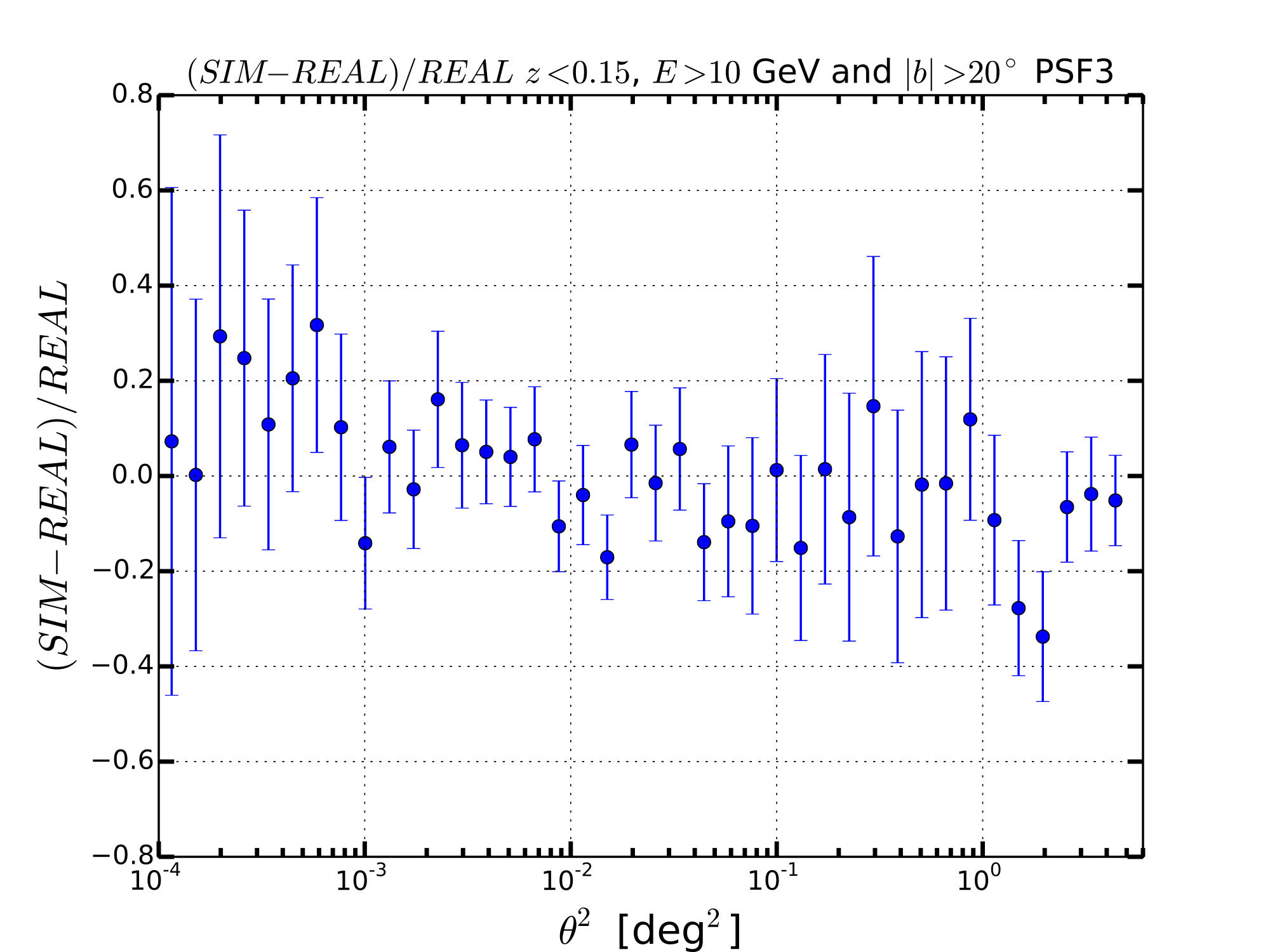
The observable that we have used is the Surface Brightness Profile (SBP) represented as dN/dtheta2 where theta is the offset angle with respect to the center of the sources. We have calculated the SBP for the real sky and the average for the 30 simulations. The average value of the SBP for each value of theta2 has been derived from the mean while the error is given by the standard deviation. This hypothesis is valid if the SBP for each value of is distributed with a Gaussian distribution. Below I show some examples that confirm this hypothesis is true.
Figure: Distribution of dN/dtheta2 for the 30 simulations for different cases (blue points) together with the Gaussian distribution (black solid line) described by the standard deviation and mean given by the SBP of the simulations.
RESULTS
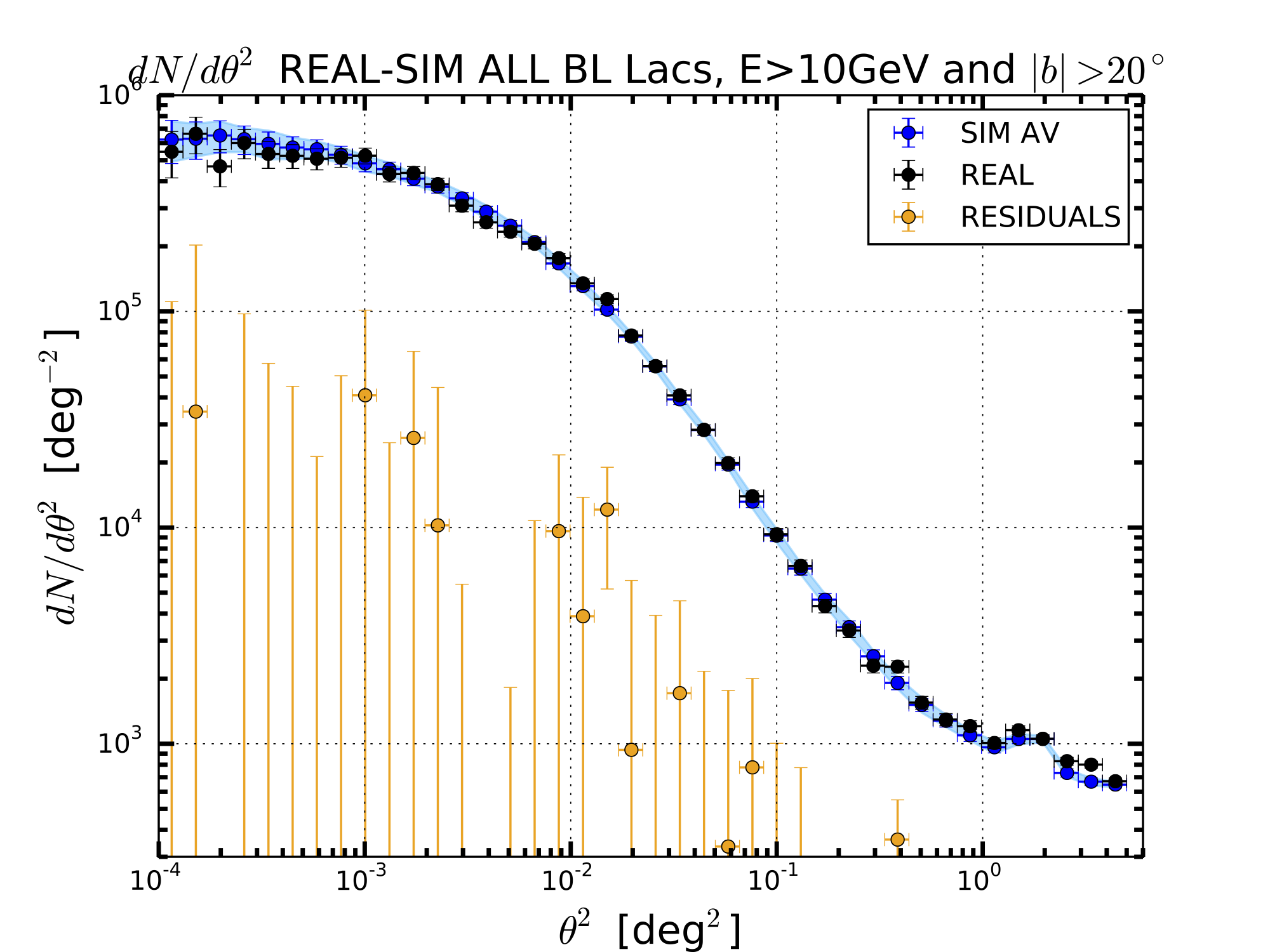
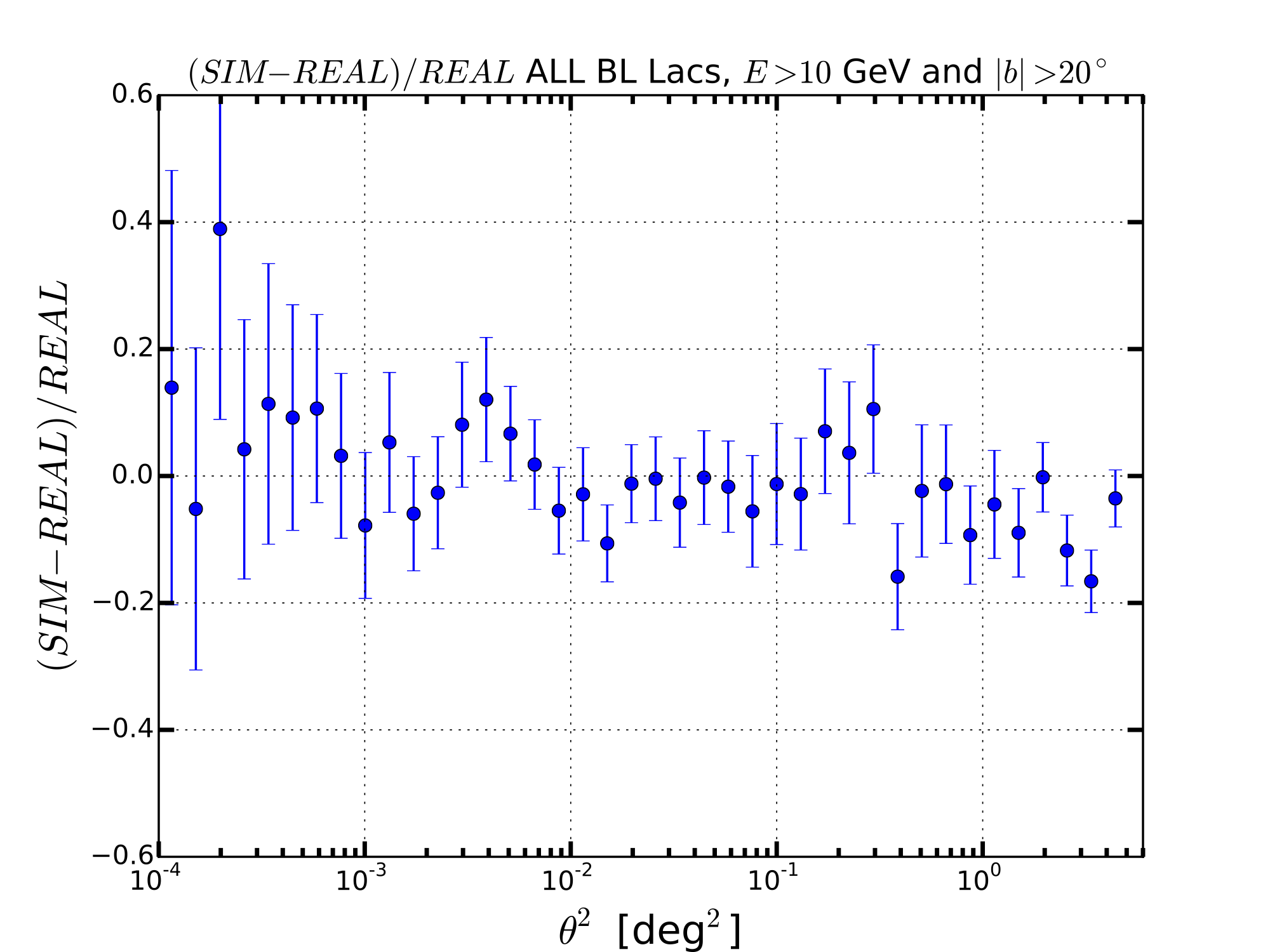
ALL WITH E>10 GeV
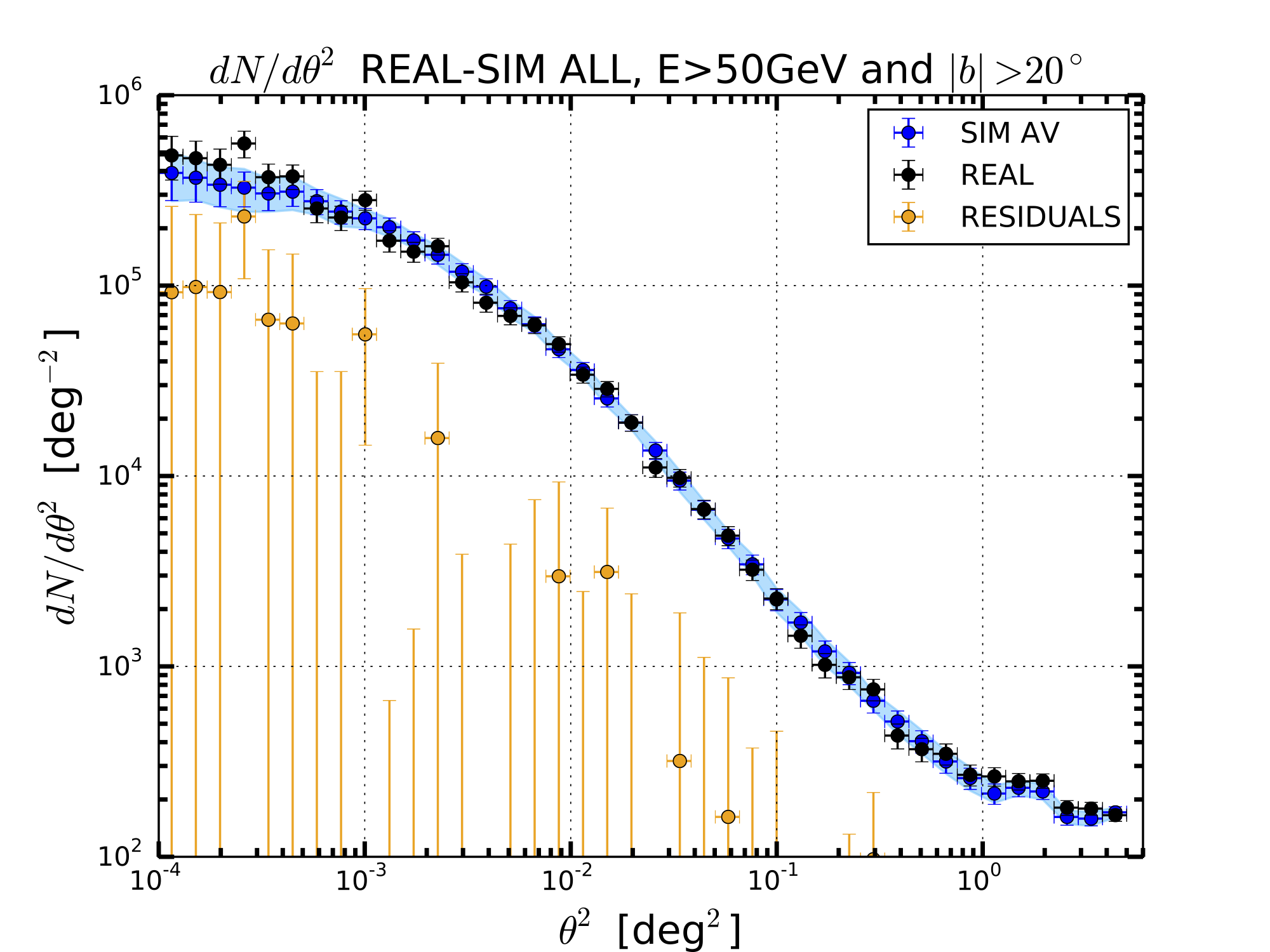
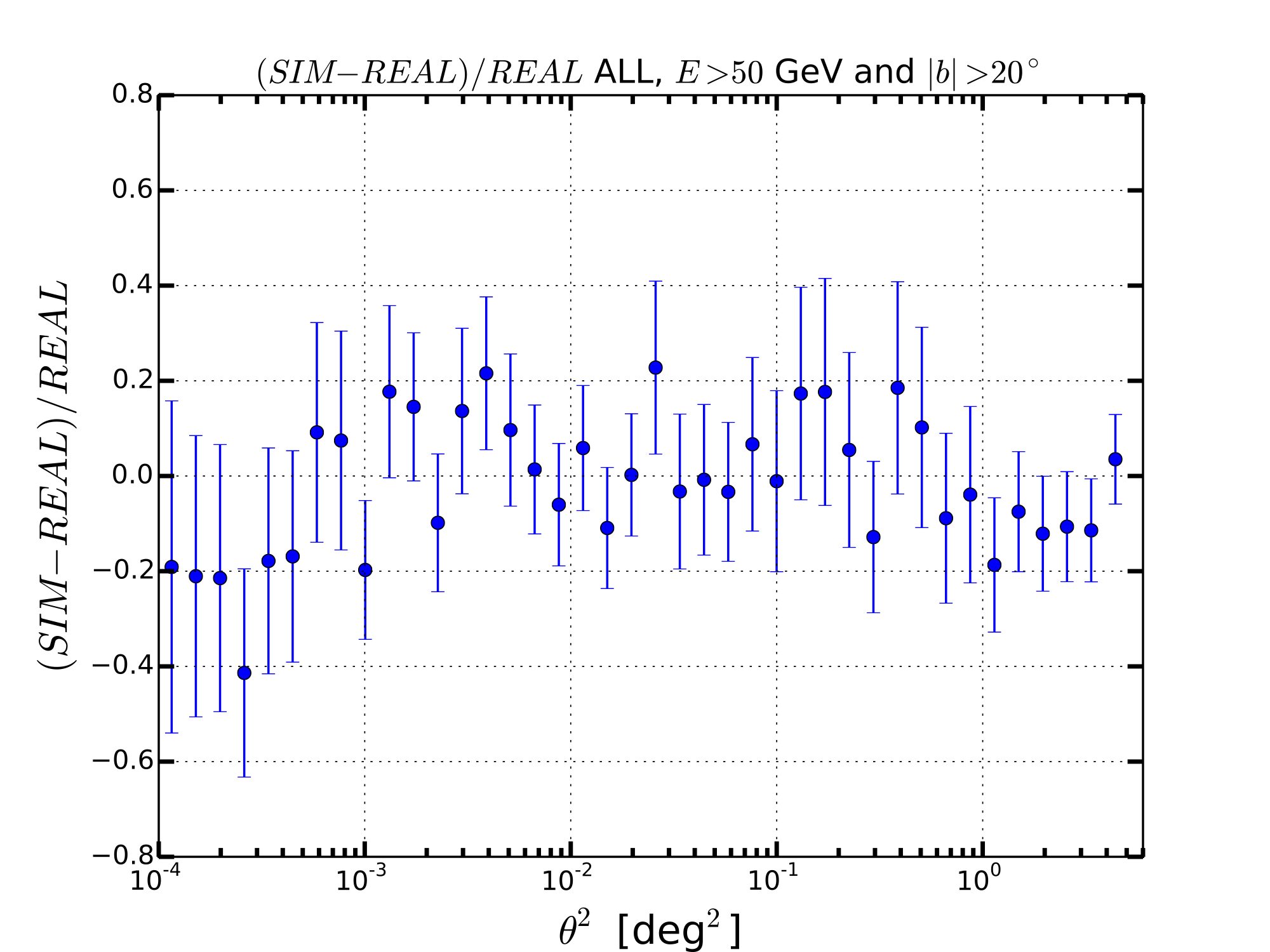
ALL WITH E>50 GeV
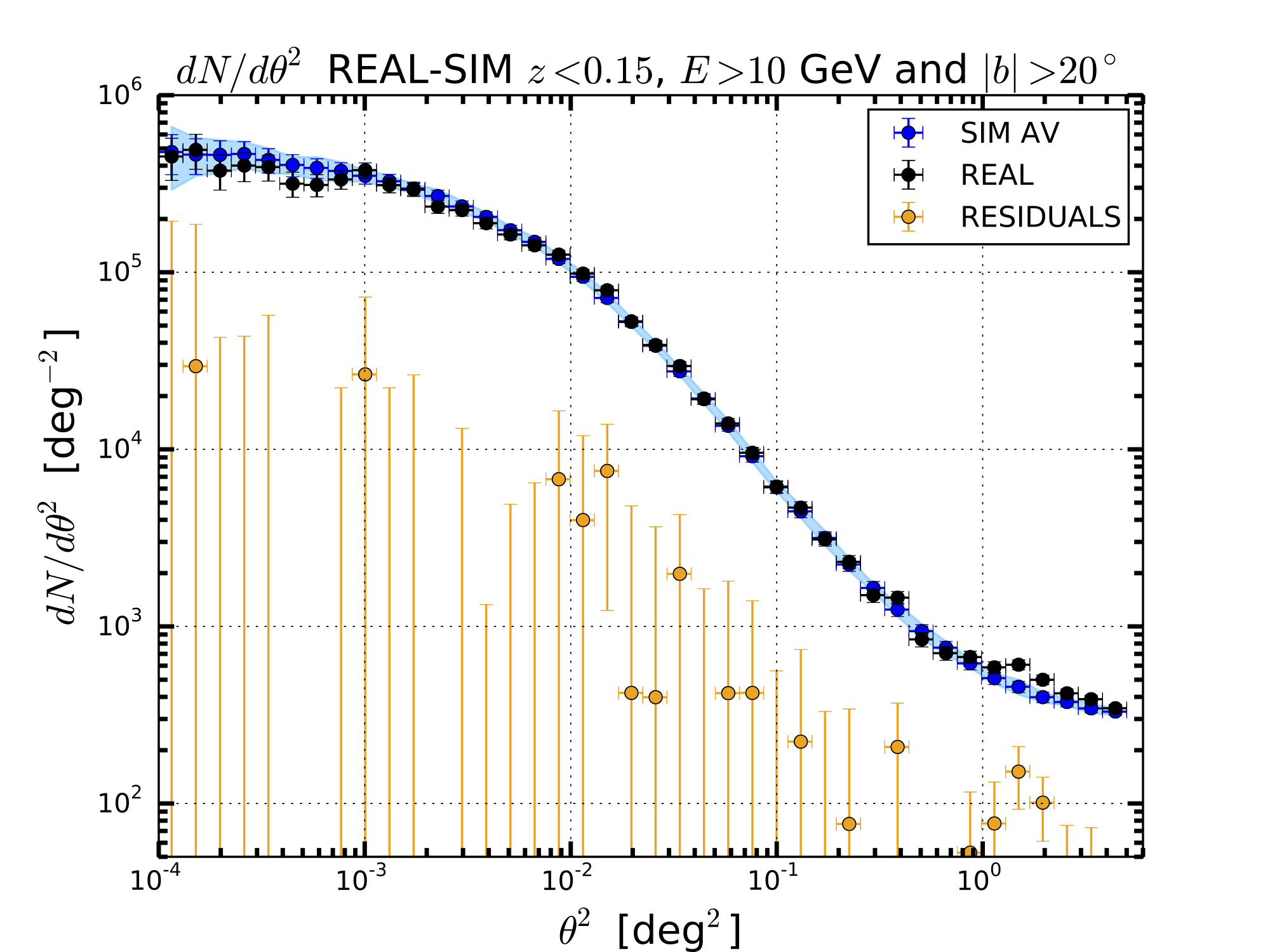
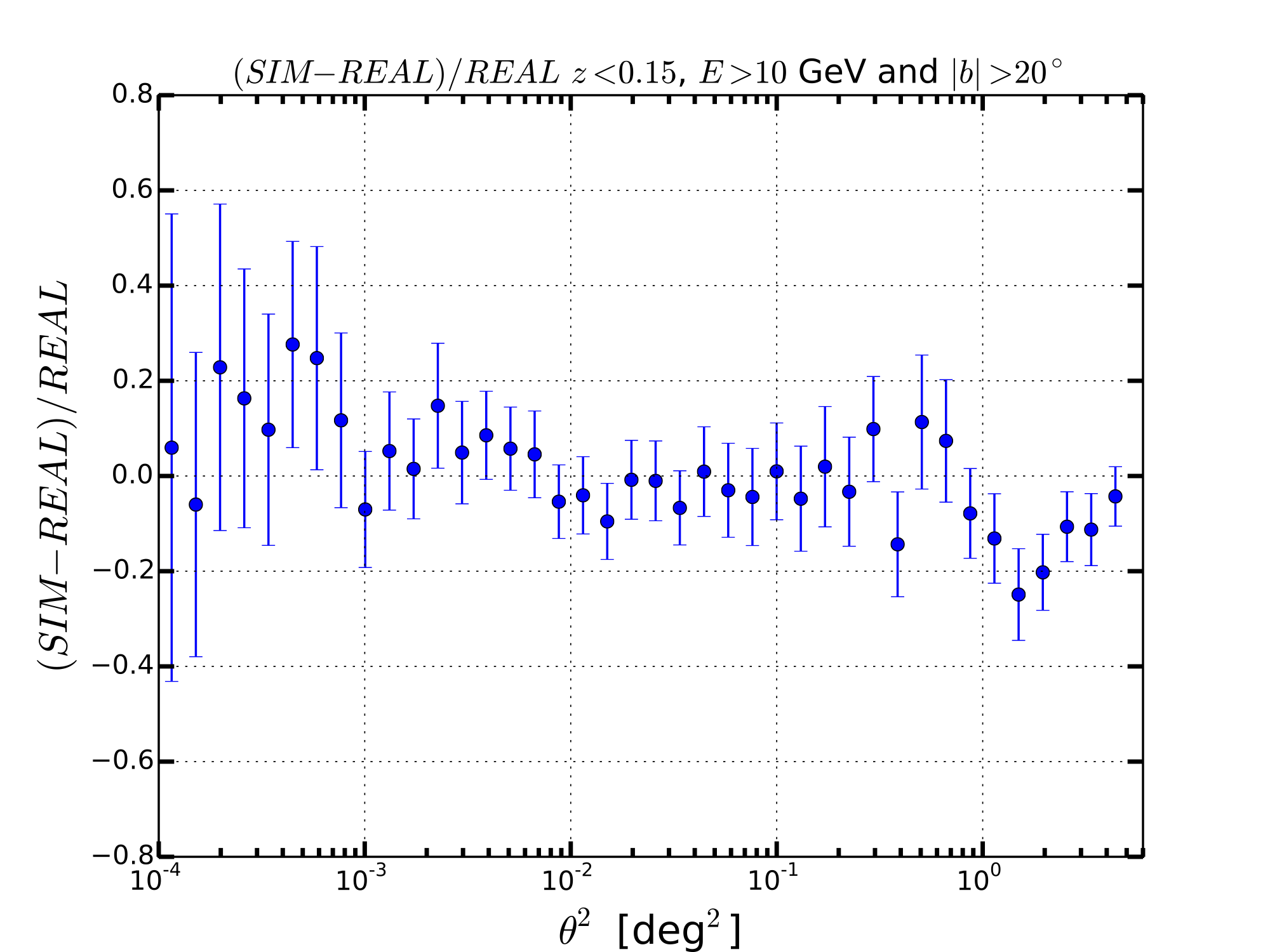
LOWZ WITH E>10 GeV
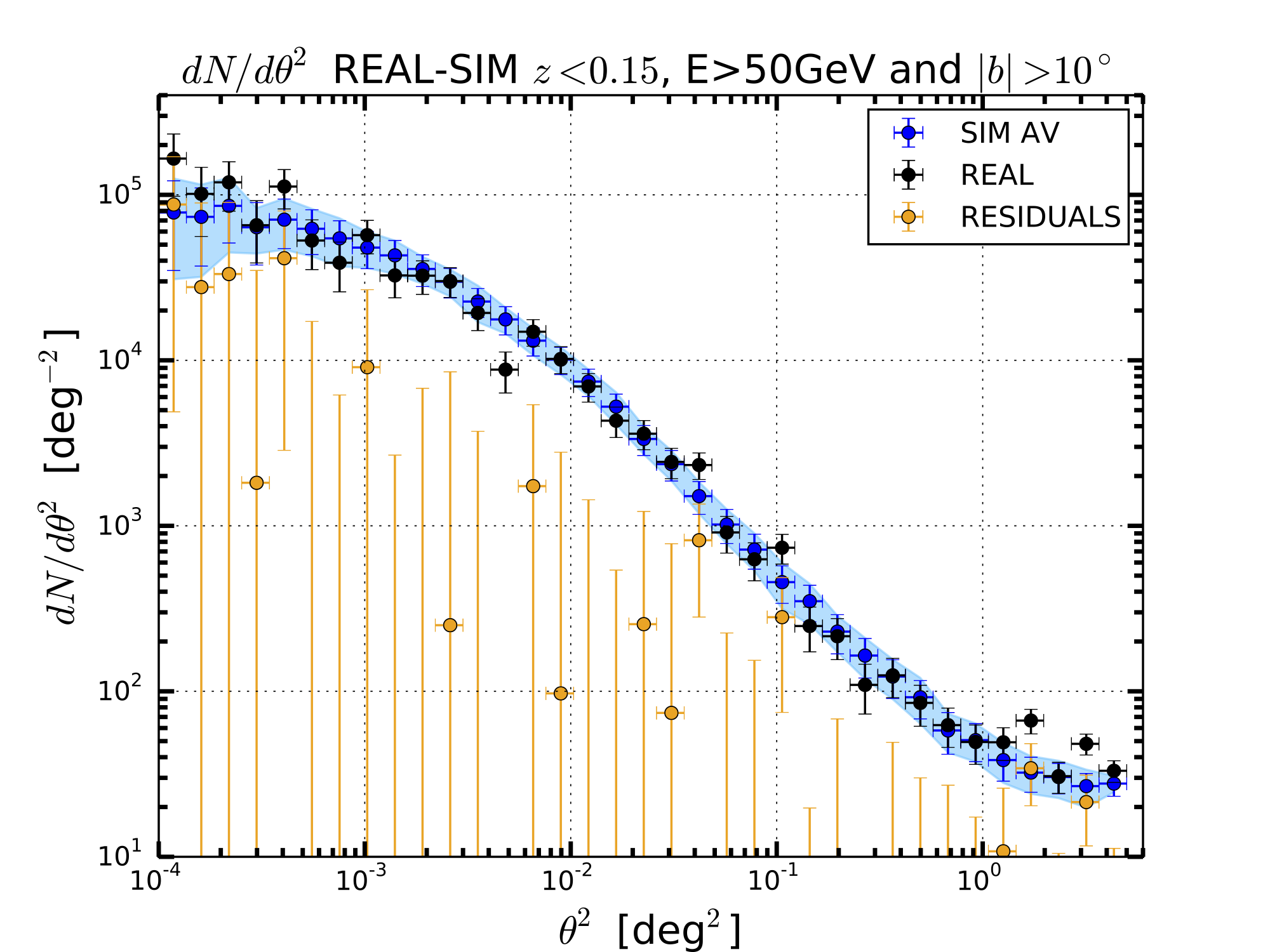
LOWZ WITH E>50 GeV
HIGHZ WITH E>10 GeV
HIGHZ WITH E>50 GeV
PSF3 AND PSF2+3 CASE
We have also tried to consider the events associated to PSF2 and PSF2+3 and for these events we have derived the SBP as given above.
-PSF 2
-PSF 2+3
STATISTICAL ANALYSIS
In the table below I report the value of the chi-square comparing the real SBP with the mean and 1sigma band of the simulation SBP. In parenthesis I show also the number of points.
I have also considered a Two Sample Kolmogorov-Smirnov Test to test if the real and simulated SBP have the same distribution.
| E>10GeV chi-square (Npoints) | E>50GeV chi-square (Npoints) | E>10GeV KS pvalue | E>50GeV KS pvalue | |
|---|---|---|---|---|
| Low z | 33.6 (35) | 36.3 (30) | 0.999 | 0.967 |
| High z | 38.5 (35) | 32.6 (25) | 0.983 | 0.936 |
| All | 37.1 (35) | 42.1 (35) | 0.983 | 0.893 |
| 50 GeV | Low z | High z | All |
|---|---|---|---|
| Simulation | 36.3 | 32.6 | 42.1 |
| Fitted Sim | 32.7 | 28.0 | 41.1 |
| Fit Sim+Halo | 30.4 | 28.0 | 41.1 |
| 10 GeV | Low z | High z | All | PSF3+2 Low z |
|---|---|---|---|---|
| Simulation | 33.6 | 38.5 | 37.1 | 31.6 |
| Fitted Sim | 33.5 | 37.6 | 36.7 | 31.4 |
| Fit Sim+Halo | 31.3 | 35.3 | 35.5 | 27.5 |
The results of this analysis is that the simulated SBP in consistent with the real sky SBP and they come from the same distribution with a pvalue>0.90.