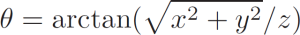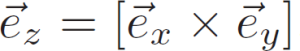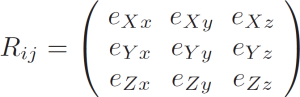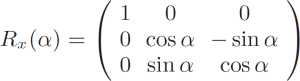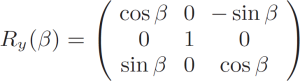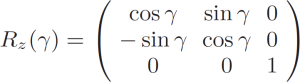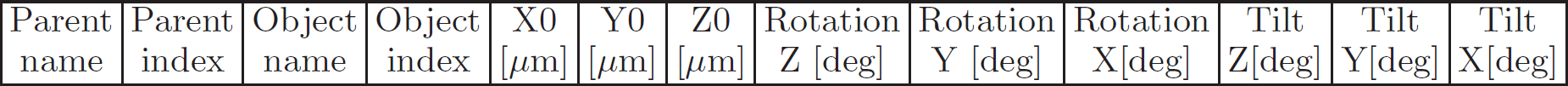Page History
...
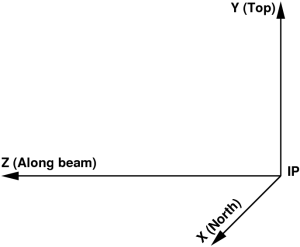
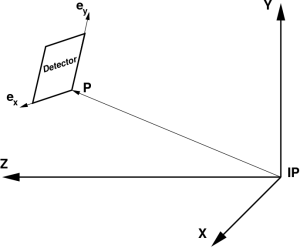
- X axis pointing from IP to the north,
- Y axis pointing from IP to the top, and
- Z axis pointing from IP along the photon beam propagation direction,
as shown in the plot:
FIG. 1: Tentative coordinate frame of experimental setup.
In this frame photon-hit pixel coordinates (x, y, z) can be easily transformed to the photon diffraction angle θ,
(1)
Sensor
On the very bottom level of hierarchy structure there should be self-sufficient components of the detector - sensors a.k.a. tiles, segments, pixel arrays/matrix etc. We assume that
- tiles may be of different types even in a single detector,
- all tiles of the same type have identical geometry,
- by design each tile has well defined geometry of pixels which does not need in calibration,
- pixel center (x, y, z) coordinates in each tile can be defined as a look-up table for all pixels,
- each tile is represented in data as a minimal solid block of memory,
- “natural” matrix-style pixel numeration is preferable for simplicity of the tile description but is not necessarily required.
For example, CSPAD 2x1 tile pixel geometry is schematically shown belowin Fig.2.
FIG. 2: Coordinate frame of CSPAD 2x1 sensor.
The CSPAD 2x1 tile has
- 185 rows and 388 columns of pixels,
- regular pixel size is 109.92 × 109.92 μm²,
- pixel size in two middle columns 193 and 194 is 274.80 × 109.92 μm².
...
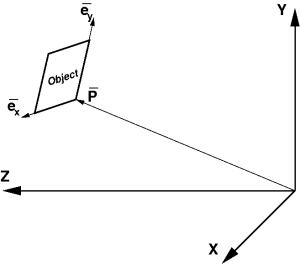
Full description of a composite detector (beside top and bottom level hierarchical objects) needs in definition of intermediate objects with their arbitrary location and orientation. Any geometry object coordinate system may have a translation and rotation with respect to the parent object, which can be defined by the 3 vectors in the setup frame as shown in Figure
FIG. 3: Child object position in the parent coordinate frame.
where
- P is a translation vector pointing from parent to its child frame origin,
- ex is a unit vector along the child frame x axis,
- ey is a unit vector along the child frame y axis.
Third unit vector ez is assumed to be right-hand triplet component, . Components of these three unit vectors form the rotation matrix
(2)
where index “j” enumerates unit vectors in the object coordinate frame, and index “i” is an object unit vector component in the parent frame (ex.: eYz is a Y component of the vector ez). Within this definition 3-d pixel coordinate “c” in the object frame can be transformed to the parent coordinate frame “C” using equation
Ci=Rij·cj + Pi. (3)
For practical reason we parametrize rotation matrix Rij in terms of Cardan’s angles R(α, β, γ). We assume that the 3-d rotation matrix R(α, β, γ) is a product of three 2-d rotations
R(α, β, γ) = Rx(α) · Ry(β) · Rz(γ), (4)
around appropriate axes, defined as
(5)
This transformation algorithm is implemented in class PSCalib.GeometryObject as discussed below.
...
- CSPAD 2x1 sensor (Fig. 2) is the low-level object with completely specified geometry of pixels.
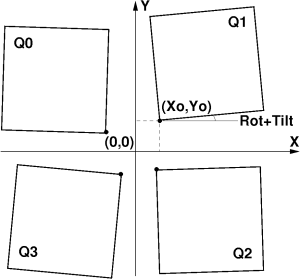
- A group of eight cspad 2x1 sensors forms a quad (Fig. 4). Sensors’ positions in the quad can be measured by optical microscope.
- Four quads form a CSPAD detector. In CXI-like CSPAD quads can be moved by the stepping motor. For technical reason this detector can not be measured with optical microscope. Dedicated runs with bright images of test wires, diffraction rings, or Bragg peaks can be used to calibrate relative quad positions. Then, quads’ position variation by the stepping motor can be accounted for once calibrated quads.
- Finally, detector position relative to IP should be accounted (Fig. 6). Detector position and orientation can be measured by the ruler in the hatch for the first approximation. The same dedicated runs with bright images can be used to evaluate precise detector coordinates. Calibration runs with a few detector positions along the beam line can be helpful for full geometry parameters reconstruction.
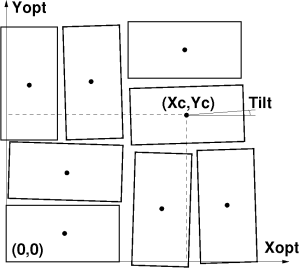
FIG. 4: Example: 2x1 sensors’ positions in the CSPAD quad coordinate frame.
FIG. 5: Example: quads’ positions in the CSPAD detector coordinate frame.
FIG. 6: Example: detector position in the experiment coordinate frame with origin at IP.
...
From metrology file we may evaluate the tile center coordinates as an average over 4 corners. Tilt angles are defined as projected angles of the tile sides on relevant planes. Each angle is evaluated as an averaged angle for 2 sides. The tile location and orientation in the parent frame can be saved in the table record where
...
...
Parent name - name and version of the parent object; all translation and rotation pars are defined w.r.t. parent Cartesian frame
...
Child geometry object pixel coordinates are transformed to the parent frame pixel coordinates in accordance with Eqn 3. We use rotation matrix expressed in terms of cosines and sines of rotation angles as shown in Eqs. 4-5 First we apply rotations around z, y, and x axes then translation. Note, that order of operations is important. This transformation algorithm is implemented in the class PSCalib.GeometryObject. For example, in Python module GeometryObject.py all transformations of pixel coordinate arrays are presented by the code
| Code Block |
|---|
#file: pyimgalgos/src/GeometryObject.py
def rotation(X, Y, C, S) :
Xrot = X*C - Y*S
Yrot = Y*C + X*S
return Xrot, Yrot
class GeometryObject :
...
def transform_geo_coord_arrays(self, X, Y, Z) :
...
# define Cx, Cy, Cz, Sx, Sy, Sz - cosines and sines of rotation + tilt angles
...
X1, Y1 = rotation(X, Y, Cz, Sz)
Z2, X2 = rotation(Z, X1, Cy, Sy)
Y3, Z3 = rotation(Y1, Z2, Cx, Sx)
Zt = Z3 + self.z0
Yt = Y3 + self.y0
Xt = X2 + self.x0
return Xt, Yt, Zt |
...
Public methods of the class PSCalib.GeometryAccess:
| Code Block |
|---|
def __init__(self, path, pbits=0) : """Constructor of the class""" def get_pixel_coords(self, oname=None, oindex=0) : """Returns three pixel X,Y,Z coordinate arrays for top or specified geometry object""" def get_pixel_areas(self, oname=None, oindex=0) : """Returns pixel areas array for top or specified geometry object""" def get_pixel_mask(self, oname=None, oindex=0, mbits=0377) : """Returns pixel mask array for top or specified geometry object. mbits =+1 - mask edges +2 - two wide-pixel central columns +4 - non-bounded pixels +8 - neighbours of non-bounded pixels""" def get_pixel_scale_size(self, oname=None, oindex=0) : """Returns pixel scale size for top or specified geometry object""" def get_dict_of_comments(self) : """Returns dictionary of comments""" def set_geo_pars(self, oname=None, oindex=0, x0=0, y0=0, z0=0, rot_z=0, rot_y=0, rot_x=0, tilt_z=0, tilt_y=0, tilt_x=0) : """Sets geometry parameters for specified or top geometry object""" def move_geo(self, oname=None, oindex=0, dx=0, dy=0, dz=0) : """Moves specified or top geometry object by dx, dy, dz""" def tilt_geo(self, oname=None, oindex=0, dt_x=0, dt_y=0, dt_z=0) : """Tilts specified or top geometry object by dt_x, dt_y, dt_z""" def print_list_of_geos(self) : def print_list_of_geos_children(self) : def print_comments_from_dict(self) : def print_pixel_coords(self, oname=None, oindex=0) : """Partial print of pixel coordinate X,Y,Z arrays for selected or top(by default) geo""" def get_pixel_coord_indexes(self, oname=None, oindex=0, pix_scale_size_um=None, xy0_off_pix=None) : """Returns three pixel X,Y,Z coordinate index arrays for top or specified geometry object""" def set_print_bits(self, pbits=0) : """ Sets printout control bitword""" def set_print_bits(self, pbits=0) : """ Sets printout control bitword""" def get_psf(self) : """Returns array of vectors in TJ format (psf stands for position-slow-fast vectors)""" def print_psf(self) : """ Gets and prints psf array for test purpose""" #------------------------------ # private methods, which may be useful: def get_geo(self, oname, oindex) : """Returns specified geometry object""" def get_top_geo(self) : """Returns top geometry object""" # global method: def img_from_pixel_arrays(iX, iY, W=None, dtype=np.float32) : """Returns image from iX, iY coordinate index arrays and associated weights W""" |
...
| Anchor | ||||
|---|---|---|---|---|
|
References
...