Synopsis
Constraint Based Geolocation (CBG) is an algorithm that is used for calculating geographical location (geolocation) of IP hosts (each host is called a target). This technique takes multiple landmarks (hosts whose lat/lon coordinates are known) as input to plot circles and identify possible regions of intersection of these circles. Each landmark is a center of a circle and the radius of a circle is the distance from a landmark to the target. The raidal distance of each circle is calculated from the minimum Round Trip Time (RTT) between a landmark and the target. RTTs are gathered from pings.
There are two variants of this technique:
- CBG multilateration: This technique uses multiple landmarks (usually 15 or more).
- CBG trilateration: This technique uses only three landmarks.
A paper regarding this study can be found here.
Motivation for integrating CBG with TULIP
CBG is found to be relatively much more accurate than other existing techniques including TULIP, Apollonius and TBG. TULIP and Apollonius are already deployed at SLAC. TBG proved not to be of much use. Thus this makes CBG integration into the current infrastructure a matter of high priority.
SLAC maintains a database for more than 540 landmarks from three different international infrastructures (PlanetLab, PingER and PerfSONAR), which cover over 99% of the world's internet population. Integration of CBG will enable us to display more accurate results for targets and consequently use this infrastructure to the best of its ability. Furthermore this will provide an amalgamation of best known geolocation techniques for research and education purposes. This can also be a very useful tool for pursuing future projects in locating IP hosts. The world is already into a transition from relatively fixed computers to mobile devices. This can potentially open a gateway for accurate locating services that can have multiple uses. A particular interesting case can be found here.
Objectives and Requirements
CBG algorithm is currently implemented in Matlab code. Whereas TULIP and Apollonius deployment at SLAC is Java based. We will integrate the two such that TULIP and Apollonius will keep running at SLAC and there'll be a Matlab server at SEECS running CBG code. There are two things which we need to take care of:
- Integration should be transparent i.e. the end user will execute the TULIP GUI as before without any changes.
- Integration should introduce minimum possible changes into the current TULIP architecture.
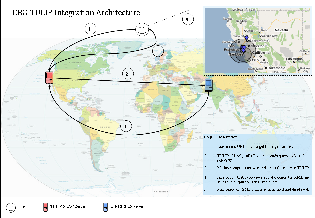
Proposed Architecture
Execution steps:
- User enters the URL with target to be geolocated.
- The TULIP visualization GUI on the client calls the Java code. The Java code calls the reflector RTT server with the target and information on the selection of landmarks . The reflector calls the enabled landmarks from the set of selected landmarks. The landmarks measure the ping RTTs to the target and return the results of the pings to the reflector, that in turn returns those results to the client. The client then massages the results and ssndscompute the answer and meanwhile sends a query string via a web service/remote routine to the Matlab server.
- The client's Java code massages the results and sends them to the Matlab server. The Matlab server computes an answer from data provided in the query string. Matlab server sends back a reply in the form of a dataset.
- The Java code receives the reply and merges this to other results to create a standardized XML file.
- This XML file is then read by TULIP visualization GUI to display the result on Google map. Each algorithm's result is represented in a distinct fashion.
This above is illustrated below in a diagram:
Matlab implementation
Package for Matlab implementation contains the code. To run the code:
- Install Matlab
- Run cbg_soi.m for constraint based on Speed of Internet (SOI), which is here defined as the speed of optical signals in fibre or ~2/3 the Speed of Light in vacuum (c).
- Run bestline.m for constraint based on bestline approach. The bestline is defined in the Constraint-Based Geolocation paper, but basically is the tightest fit over all the (delay, distance) pairs meant to never underestimate the distance for a delay.
- Rest can be found in README.txt file provided with the package.