Quickstart

The timetool is used to measure the inherent jitter in the arrival time between an optical laser and LCLS x-ray pulse. In most cases, if the timetool has been set up properly, it is possible to simply use the DAQ's default analysis to extract this difference in arrival time. You will still need to calibrate the timetool: read the section on calibration to understand why and how. Then you can blindly use the results provided by LCLS. Lucky you! The information here on how the timetool works may still be of interest, and if you have decided to just trust the DAQ, you have a lot of free time on your hands now – so why not learn about it?

In many cases, however, re-processing of the timetool is desirable. Maybe the tool was not set up quite right, and you suspect errors in the default analysis. Or you are using 3rd party software that needs to process the raw signal for some reason. Or you are a hater of black boxes and need to do all analysis yourself. If you wish to re-process the timetool signal, this page explains how the 'tool works, and presents the use of psana-python code that can assist you in this endeavor. That code can probably do what you want, and can act as a template if it does not.

Enough rambling. To femtoseconds!... ok ok but not beyond.

Principle of Operation

Before embarking on timetool analysis, it is useful to understand how the thing works. Duh. The TT signal comes in the form of a 2D camera image, one for each event (x-ray pulse). The tool measures the time difference between laser and FEL by one of two methods:

spatial encoding (also called "reflection" mode), where the X-rays change the reflectivity of a material and a laser probes that change by the incident angle of its wavefront; or
spectral encoding (also called "transmission" mode), where the X-rays change the transmission of a material and a chirped laser probes it by a change in the spectral components of the transmitted laser.

Nearly all experiments use option #2. If you are running in option #1, ignore the rest of this page and get help (ask your PoC). I will proceed describing mode 2.

A "timetool" is composed of the following elements:

A laser setup that creates a chirped white-light ps-length pulse concurrently with the pump
A "target", usually YAG or SiNx, that gets put in the path of both the white light and LCLS x-ray beam
A diffraction grating that disperses the white light pulse after it goes through the target
A camera that captures the dispersed white light

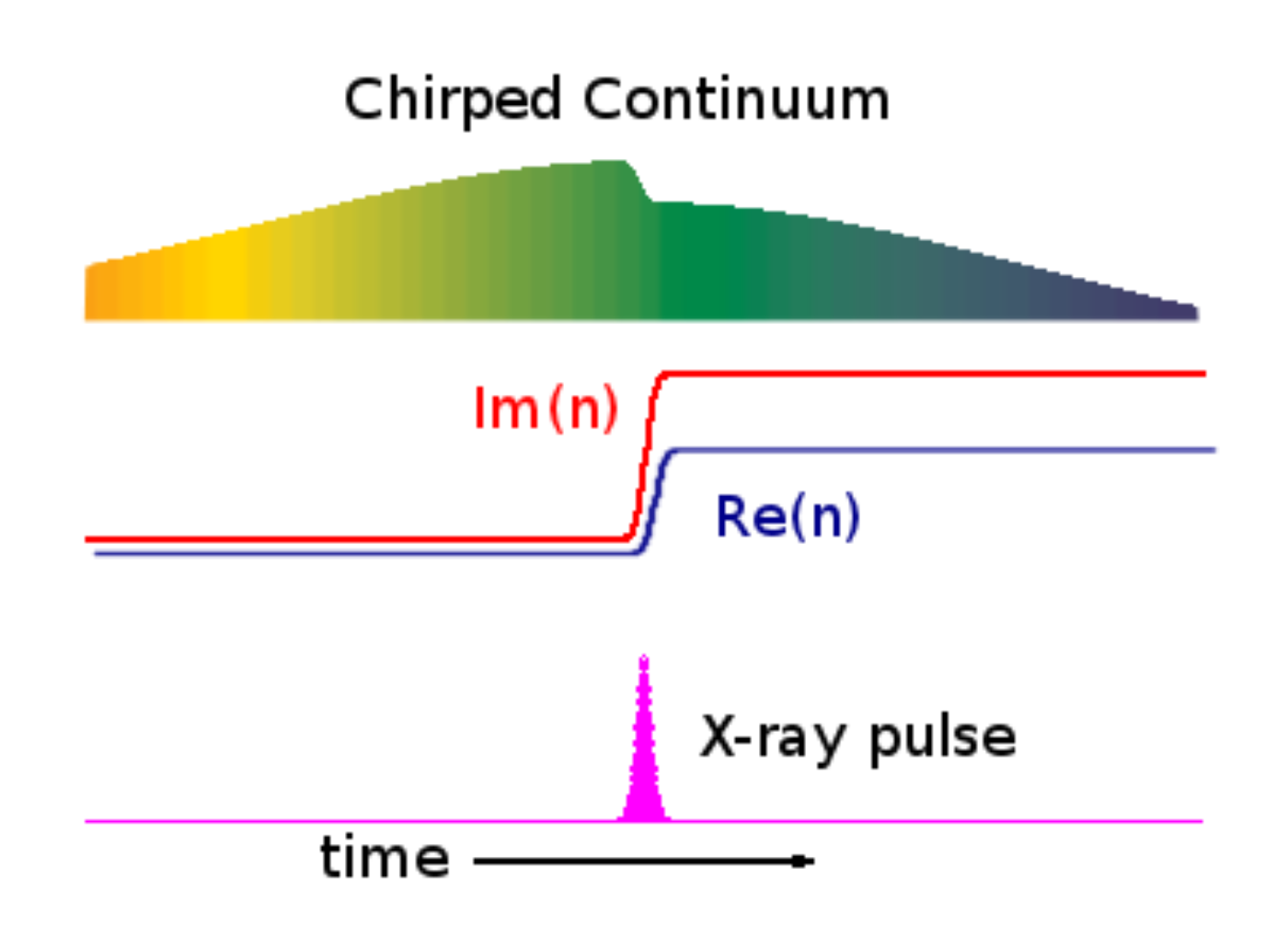
The white light propagates through the target, with shorter (bluer) wavelengths arriving first, and longer (redder) wavelengths arriving later. Somewhere in the middle of passing through the target, the x-rays join the party, hitting the target at the same place, but for a shorter temporal duration (~50 fs is typical). This causes the index of refraction of the material to change, and generates an edge in the white light power profile (in time, and therefore also spectrally, due to the chirp). See figure:

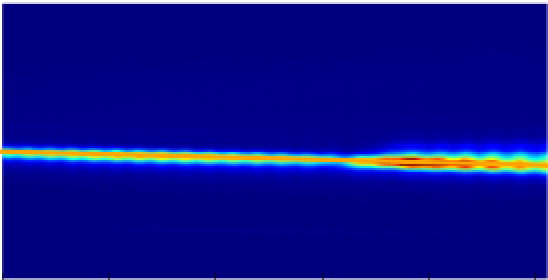
The white light, now "imprinted" with the x-ray pulse, is dispersed by a diffraction grating onto a camera. Here's what the raw signal looks like, typically:

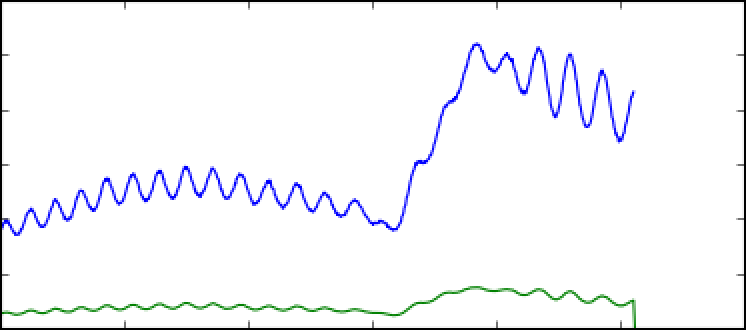
If you take a projection of this image along the y-axis, you obtain a trace similar to this:

The blue line is a raw projection, the green is an ROI'd projection (recommended!). A few things to notice:

Boom! An edge! The edge moves back and forth on the camera screen depending on the relative time delay between the laser and x-rays.
Wiggles. The nearly-constant sine-like wave is undesirable background due to an etalon effect inside the TT target. Good analysis will remove it (read on). The etalon is especially bad here – it's amplitude and frequency will depend on the target.
Limited dynamic range. The edge is big with respect to the camera. The TT has about ~1 ps of dynamic range in a given physical setup. That's fine, because the typical jitter in arrival times between x-rays and laser at LCLS is much less than that. Also, the white light pulse is only ~1 ps long! To change the delay "window" the TT is looking at, a delay stage is used to move the white light in time to keep it matched to the x-rays. It is important, however, to keep an eye on the TT signal and make sure it doesn't drift off the camera!
Read right-to-left. In this image, the white light arriving before the x-rays is to the right, and following it in time takes us to the left. So time is right to left. Just keeping you on your toes.

How does knowing the arrival time of the white light tell us the x-ray/laser time delay?

One confusing aspect for new users of the timetool is that there are a lot of laser pulses to keep track of. For any timetool setup, there will be at least three:

A femtosecond "pump" laser
The white-light ps pulse used for the timetool
The fs x-ray pulse delivered by the LCLS

The first two are generated in the hutch (or nearby) by the same laser process. That means that there is a fixed, known time delay between the two. Also, that delay can be controlled using a delay stage.

The timetool strategy is as follows. Imagine we start with all three pulses overlapped in time (up to some unknown jitter). Then, we set the femtosecond laser trigger to the desired delay – for instance, say, 2 ps before the arrival of the x-rays. The white light will also now arrive 2 ps before the x-rays. So we drive the delay stage (which is on the white light branch only) to move the white light 2 ps earlier. Now, the white light is overlapped with the x-rays once more! Further, we know the time difference between the fs laser and white light is exactly 2 ps.

The white light can now be used as part of the timetool, as described. Measuring the jitter in delay between it and the x-rays will also give us the jitter between the fs laser and x-rays, even though the latter two are not temporally overlapped.

The jitter problem is inherent in such a large machine as the LCLS. The x-ray pulse is generated waaay upstream (starting ~1 km away) and so, despite the best efforts of the laser guys, they will probably never be able to perfectly time their lasers – which originate in the hutches – to the LCLS pulse. So instead we use the timetool.

Default Analysis: DAQ

Timetool results can be computed by the DAQ while data is being recorded and written directly into the .xtc files. This is almost always done. The DAQ's processing algorithm is quite good, and most users can employ those results without modification. This section will detail how the DAQ's algorithm works, access those results, assess their quality. Even if you are going to eventually implement your own solution, understanding how this analysis works will be useful. Further, in almost all cases, the DAQ results are good enough for online monitoring of the experiment.

How it works

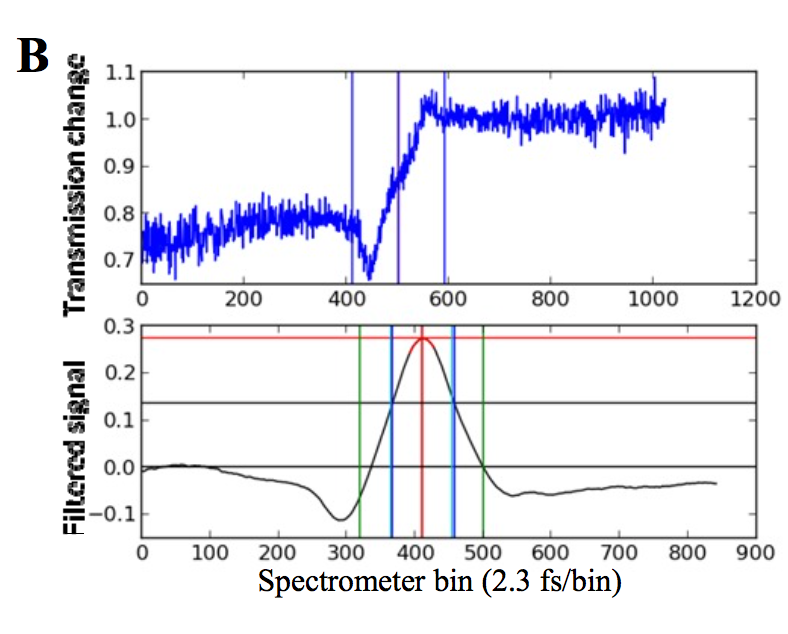
The goal is to find the edge position, the imprint of the x-rays on the white light pulse, along the x-axis of the OPAL camera. To do this, the DAQ uses a matched filter – that means the filter looks just like the expected signal (an edge) and is "translated" across the signal, looking for the x-position of maximal matchy match. More technically: the filter is convoluted with the signal, and the convolution has a peak. That peak is identified as the edge "position" and gives your time signal. Here is an example of a TT trace (top) and the resulting convolution (bottom) used to locate the edge:

The FWHM of the convolution and it's amplitude are good indicators of how well this worked, and are also reported.

Where do the filter weights come from?

From Matt Weaver 8/23/17: (including extra thoughts transcribed by cpo from Matt on 02/26/20)

The spectrum ratio is treated as a waveform, and that waveform is analyzed with a Wiener filter in the "time" domain. It is actually a matched filter where the noise is characterized by taking the ratio of non-exposed spectra from different images - should be flat but the instability of the reference optical spectrum causes it to have correlated movements. So, the procedure for producing those matched filter weights goes like this:

Collect several non-xray exposed spectra ("dropped shots" or "event code 162")
Define an ROI (e.g. 50 pixels) around the signal region. use this ROI for all calculations below, although it has to move to follow the location when the average signal is computed (step 5). Matt says it's not so scientific how one obtains this "averaged signal": one could find several events, center the edge in a window, and then take an average of as many events as it takes for it to "look good". Or just take one event and smooth out the background somehow. He did the latter when he computed the weights.
for each background shot divide by the background averaged over many shots ("normalize")
calculate the auto-correlation function ("acf") of those normalized waveforms. One correlates each sample with each sample n-away in the same waveform creating an array of the same size as the input waveform. The acf is the average of all those products.
Collect your best averaged ratio (signal divided by averaged background) with signal; this averaging smooths out any non-physics features

There's a script (https://github.com/lcls-psana/TimeTool/blob/master/data/timetool_setup.py) which shows the last steps of the calibration process that produces the matched filter weights from the autocorrelation function and the signal waveform. That script has the auto-correlation function and averaged-signal hard-coded into it, but it shows the procedure. It requires some manual intervention to get a sensible answer, since there are often undesirable features in the signal that the algorithm picks up and tries to optimize towards. The fundamental formula in that script is weights=scipy.linalg.inv(scipy.linalg.toeplitz(acf))*(averaged_signal).

The above procedure optimizes the filter to reject the background. Matt doesn't currently remember a physical picture of why the "toeplitz" formula optimizes the weights to reject background. If one wants to simplify by ignoring the background suppression optimization, the "average signal" (ignoring the background) can also be used as a set of weights for np.convolve.

The astute reader will notice that this trace has no etalon wiggles. That is because it has been cleaned up by subtracting an x-ray off shot (BYKICK). Those events have the same etalon effect, but no edge – subtracting them removes the etalon. That's a good thing, because the etalon wiggles would have given this method a little trouble if they were big in amplitude.

So, to summarize, here is what the DAQ analysis code does:

Extract the TT trace using an ROI + projection
Subtract the most recent x-ray off (BYKICK) trace
Convolve the trace with a filter
Report the position, amplitude, FWHM of the resulting peak

The reported position will be in PIXELS. That is not so useful! To convert to femtoseconds, we need to calibrate the TT.

Important Note on How to Compute Time Delays

The timetool only gives you a small correction to the laser-xray delay. The "nominal" delay is set by the laser, which is phase locked to the x-rays. The timetool measures jitter around that nominal delay. So you should compute the final delay as:

delay = nominal_delay + timetool_correction

Since different people have different conventions about the sign that corresponds to "pump early" vs. "pump late" you must exercise caution that you are doing the right thing here. Ensure that things are what you think they are. If possible, figure this out before your experiment begins, or early in running, and write it down. Force everyone to use the same conventions. Especially if you are on night shift :).

The "nominal delay" should be easily accessible as a PV. Unfortunately, it will vary hutch-to-hutch. Sorry. Ask your beamline scientist or PCDS PoC for help.

How to get the results

Results can be accessed using the following epics-variables names:

TTSPEC:FLTPOS	the position of the edge, in pixels
TTSPEC:AMPL	amplitude of biggest edge found by the filter
TTSPEC:FLTPOSFWHM	the FWHM of the edge, in pixels
TTSPEC:AMPLNXT	amplitude of second-biggest edge found by the filter, good for rejecting bad fits
TTSPEC:REFAMPL	amplitude of the background "reference" which is subtracted before running the filter algorithm, good for rejecting bad fits
TTSPEC:FLTPOS_PS	the position of the edge, in picoseconds, but requires correct calibration constants be put in the DAQ when data is acquired. Few people do this. So be wary.

These are usually pre-pended by the hutch, so e.g. at XPP they will be "XPP:TTSPEC:FLTPOS". The TT camera (an OPAL) should also be in the datastream.

Here is an example of how to get these values from psana

Accessing TT Data in psana (python)

import psana

ds = psana.MPIDataSource('exp=cxij8816:run=221')

evr       = psana.Detector('NoDetector.0:Evr.0')
tt_camera = psana.Detector('Timetool')
tt_pos    = psana.Detector('CXI:TTSPEC:FLTPOS')
tt_amp    = psana.Detector('CXI:TTSPEC:AMPL')
tt_fwhm   = psana.Detector('CXI:TTSPEC:FLTPOSFWHM')

for i,evt in enumerate(ds.events()):
    tt_img = tt_camera.raw(evt)
	# <...>

How to know it did the right thing

Cool! OK, so how do you now if it worked? Here are a number of things to check:

Plot some TT traces with the edge position on top of them, and make sure the edge found is reasonable.
Look at a "jitter histogram", that is the distribution of edge positions found, for a set time delay. The distribution should be approximately Gaussian. Not perfectly. But it should not be multi-modal.
Do pairwise correlation plots between TTSPEC:FLTPOS / TTSPEC:AMPL / TTSPEC:FLTPOSFWHM, and ensure that you don't see anything "weird". They should form nice blobs – maybe not perfectly Gaussian, but without big outliers, periodic behavior, or "streaks".
Analyze a calibration run, where you change the delay in a known fashion, and make sure your analysis matches that known delay (see next section).
The gold standard: do your full data analysis and look for weirdness. Physics can be quite sensitive to issues! But it can often be difficult to trouble shoot this way, as many things could have caused your experiment to screw up.

Outliers in the timetool analysis are common, and most people typically throw away shots that fall outside obvious "safe" regions. That is totally normal, and typically will not skew your results.

Filtering TT Data

If you make a plot of the measured timetool delay it is quite noisy (e.g. the laser delay vs. the measured filter position, TTSPEC:FLTPOS, while keeping the TT stage stationary). There are many outliers. This can be greatly cleaned up by filtering based on the TT peak.

I (TJ, <tjlane@slac.stanford.edu>) have found the following "vetos" on the data to work well, though they are quite conservative (throw away a decent amount of data). That said they should greatly clean up the TT response and has let me proceed in a "blind" fashion:

Require:

tt_amp [TTSPEC:AMPL] > 0.05 AND

50.0 < tt_fwhm [TTSPEC:FLTPOSFWHM]< 300.0

This was selected based on one experiment (cxii2415, run 65) and cross-validated against another (cxij8816, run 69).

Always Calibrate! Why and How.

As previously mentioned, the timetool trace edge is found and reported in pixels along the OPAL camera (e.g. arbitrary spatial units), and must be converted into a time delay (in femtoseconds). Because the TT response is a function of geometry, and that geometry can change even during an experiment due to thermal expansion, changing laser alignment, different TT targets, etc, frequent calibration is recommended. A good baseline recommendation is to do it once per shift, and then again if something affecting the TT changes.

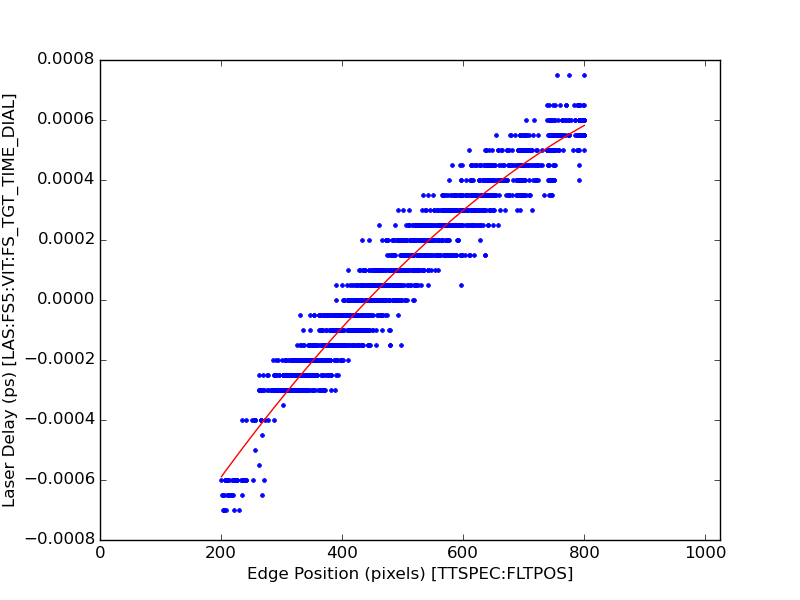
To calibrate, we change the laser delay (which affects the white light) while keeping the delay stage for the TT constant. This causes the edge to transverse the camera, going from one end to the other, as the white light delay changes due to the changing propagation length. Because we know the speed of light, we can figure out what the change in time delay was, and use that known value to calibrate how much the edge moves (in pixels) for a given time delay change.

Two practicalities to remember:

There is inherent jitter in the arrival time between x-rays and laser (remember, this is why we need the TT!). So to do this calibration we have to average out this jitter across many shots. The jitter is typically roughly Gaussian, so this works.
The delay-to-edge conversion is not generally perfectly linear. In common use at LCLS is a 2nd order polynomial fit (phenomenological) which seems to work great.

Here's a typical calibration result from CXI, with vetos applied:

FIT RESULTS
fs_result = a + b*x + c*x^2,  x is edge position
------------------------------------------------
a = -0.001196897053
b = 0.000003302866
c = -0.000000001349
------------------------------------------------
fit range (tt pixels): 200 <> 800
time range (fs):       -0.000590 <> 0.000582
------------------------------------------------

Unfortunately, right now CXI, XPP, and AMO have different methods for doing this calibration. Talk to your beamline scientist about how to do it and process the results.

Conversion from FLTPOS pixels into ps

Once you do this calibration, it should be possible to write a simple function to give you the corrected delay between x-rays and optical laser. For example, the following code snip was used for an experiment at CXI. NOTE THIS MAY CHANGE GIVEN YOUR HUTCH AND CONVENTIONS. But it should be a good starting point .

Conversion of FLTPOS into PS delay

def relative_time(edge_position):
    """
    Translate edge position into fs (for cxij8816)
    
    from docs >> fs_result = a + b*x + c*x^2, x is edge position
    """
    a = -0.0013584927458976459
    b =  3.1264188429430901e-06
    c = -1.1172611228659911e-09
    x = tt_pos(evt)
    tt_correction = a + b*x + c*x**2
    time_delay = las_stg(evt)
    return -1000*(time_delay + tt_correction)

Rolling Your Own

Hopefully you now understand how the timetool works, how the DAQ analysis works, and how to access and validate those results. If your DAQ results look unacceptable for some reason, you can try to re-process the timetool signal. If, right now, you are thinking "I need to do that!", you have a general idea of how to go about it. If you need further help, get in touch with the LCLS data analysis group. In general we'd be curious to hear about situations where the DAQ processing does not work and needs improvement.

There are currently two resources you can employ to get going:

It is possible to re-run the DAQ algorithm offline in psana, with e.g. different filter weights or other settings. This is documented extensively.
There is some experimental python code for use in situations where the etalon signal is very strong and screws up the analysis. It also simply re-implements a version of the DAQ analysis in python, rather than C++, which may be easier to customize. This is under active development and should be considered use-at-your-own-risk. Get in touch with TJ Lane <tjlane@slac.stanford.edu> if you think this would be useful for you.

References

https://opg.optica.org/oe/fulltext.cfm?uri=oe-19-22-21855&id=223755

https://www.nature.com/articles/nphoton.2013.11

https://opg.optica.org/oe/fulltext.cfm?uri=oe-28-16-23545&id=433772