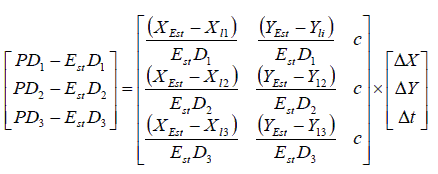TULIP Trilateration Algorithm
minRTT = propagation delay + extra delay (due to extra circular routes , congestion and router delays)
delta(T) measured= delta(t) + delta(t0)
(Pseudo-distance)
PD = delta(T) measured . alpha
(Actual distance)
D = delta(T) . alpha
PD = (delta(T) + delta(T0)). alpha
PD = D + delta(T0) .c .................................(1)
D = actual distance from the landmark.
C = speed of light
alpha = X(c) i.e. Speed of digital info in fiber optic cable
X = factor of c with which digital info travels in fiber optic cable.
delta(T) = actual propagation delay along the greater circle router/paths.
delta(T0) = the extra delay causing overestimation.
PD = pseudo distance
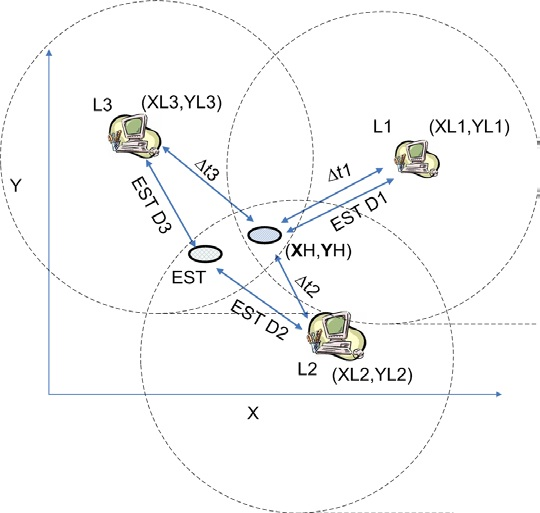
Graphically,
H: host
L1: Landmark 1
L2: landmark 2
L3: landmark 3
Using distance farmula:
D1= sqrt(XL1- Xh)^2 + (YL1 - YH)^2 ............................................. (2)
FROM (1) & (2)
PD1= (sqrt(XL1 - XH )^2 + (YL1 - YH)^2) + delta(T0) . alpha .................... (A)
Similarly for other 2 landmarks:
PD2= (sqrt(XL2 - XH )^2 + (YL2 - YH)^2) + delta(t0) . alpha .................... (B)
PD3= (sqrt(XL3 - XH )^2 + (YL3 - YH)^2) + delta(t0) . alpha .....................(C)
We need to linearize (A), (B) & (C) to solve them
Using Taylor Series:
f(x0) . ( x- x0) f ' (x0) . (x - x0)
f( x ) = f (x0) + ---------- + --------------------
1! 2!
Considering the simplified part first
f ( x ) = f (x0) + f(x0)(x - x0)
put (x-x0) = delta(x)
f ( x ) = f (x0) + f' (x0) delta ( x ) .......................(3)
Hence to compute the original value of X an arbitrary value x0 is required, this is done by simple trilateration
We know that:
Hx = X est + delta ( x )
Hy = Y est + delta ( y )
Also
Est Di = (Lhi - Xest) + (Hy - Yest) .......................(4)
From (3) and (4)
d(EstDi) . delta ( x ) d(EstDi) . delta( y )
PDi = Est Di + ---------- + -----------------
dX dY
After carrying out partial differentiation
(Xest - Xli) (Yest - Yi)
ODi = Est Di + --------. delta ( x ) + ---------------- delta ( y) + c. delta(To)
dX dY
Now we need to solve ( x , y , delta(to))
Solution from (4) is put in eq(D) to get new estimations.
Hx,Hy becomes the new estimated position
Reference
http://www.ece.cmu.edu/research/publications/2003/CMU-ECE-2003-038.pdf