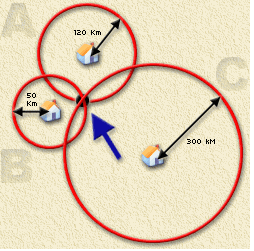
As the name suggests, the trilateration technique uses three RTT values to estimate the coordinates of target node. In the trilateration technique, when several landmarks ping the specified target, the three landmarks with smallest RTT values (probably nearest located landmarks) are selected.The algorithm then tries to estimate the location on the basis of overlapping region of the drawn circles around these selected landmarks. Figure 1 depicts this technique. In the trilateration technique, the center of the overlapping region is considered as the location of the target node.
There are many ways to implement the trilateration technique, discussed in the paper Time Of Arrival (TOA)- based trilateration method. These include:
- Linear Least Square Method
- Nonlinear Least Square Method
- Circles intersection with Clustering
- Trilateration in 2D and 3D
Previously we were implementing Linear Least Square Method to implement trilateration. With this method 50% of targets showed distance error above 1000 km. We went through a paper on Time Of Arrival (TOA)- based trilateration method which discusses the different positioning algorithms. In that paper it is mentioned that Linear Least Square Method is not very accurate and it just provides initial position which can be used in other positioning algorithms (i.e. Nonlinear Least Squares and Independent Time GPS Least Squares) as initialization value for further iterations.
We went through trilateration method as described on wikipedia and found that method to be easy and straight forward. But the algorithm mentioned was solving trilateration in 3D plane. We implemented it in 2D plane.
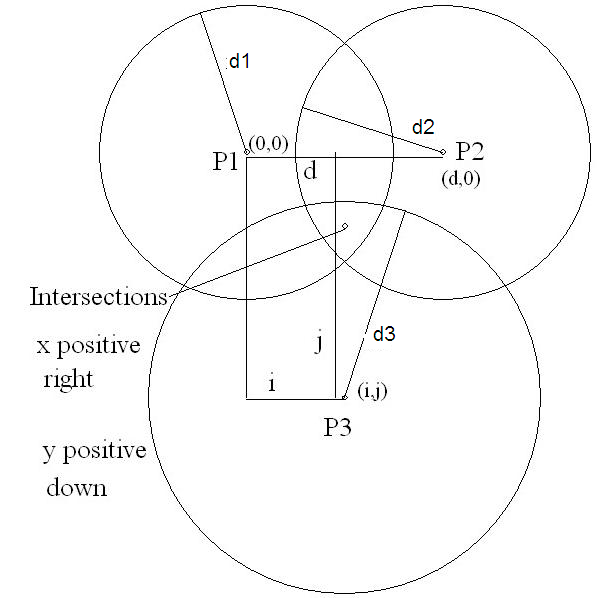
This method is based on solving equations of circle. Figure 2 below shows three circles drawn from each of three landmarks to the target. d1, d2, d3 are the radii of circles.
P1=1st Landmark position in x,y coordinates
P2=2nd Landmark position in x,y coordinates
P3=3rd Landmark position in x,y coordinates
d1= distance from 1st Landmark to target (Calculated using distance=(MinRTT/2)*alpha)
d2=distance from 2nd Landmark to target (Calculated using distance=(MinRTT/2)*alpha)
d3=distance from 3rd Landmark to target (Calculated using distance=(MinRTT/2)*alpha)
i1=P1.x,
i2=P2.x,
i3=P3.x
j1=P1.y,
j2=P2.y,
j3=P3.y
x=target x coordinate
y=target y coordinate
Lets label circles as 1,2 and 3. i1,j1 are center coordinates of circle 1, i2,j2 & i3,j3 are center coordinates for circle 2 and circle 3 respectively.
We know equation for circle
(x - h)2 + (y - k)2 = r2
where h and k are x and y coordinates of center of circle.
x and y in above equation are x and y intercept of circle.i.e where circle has intersection with x-axis and y-axis.
and r is radius.
Using Equation for circles and solving the above figure
x =
{ ( [ (d1^2-d2^2) + (i2^2-i1^2) + (j2^2-j1^2) ] * (2*j3-2*j2) - [ (d2^2-d3^2) + (i3^2-i2^2) + (j3^2-j2^2) ] *(2*j2-2*j1) ) /
[ (2*i2-2*i3)(2*j2-2*j1)-(2*i1-2*i2)(2*j3-2*j2 ] }
y = [ (d1^2-d2^2) + (i2^2-i1^2) + (j2^2-j1^2) + x*(2*i1-2*i2)] / (2*j2-2*j1)
x,y are the required coordinates of a Point (Target)
Results
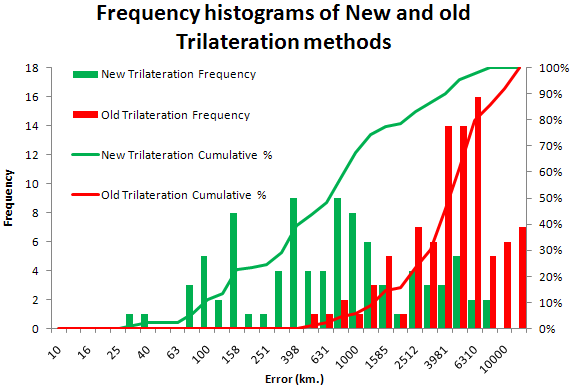
The performance of trilateration has improved dramatically as shown in Figure 3 below for 87 targets in 16 countries:
The histograms of the 2 frequency distributions is shown below. The details are found in the spreadsheet .